The cylinder rolls
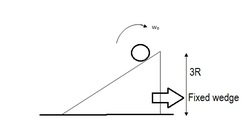 A spinning cylinder with angular velocity
of Mass
and radius
is lowered on a rough fixed wedge of angle
with the horizontal and coefficient of friction
. The cylinder is released at a height of
from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline in
A spinning cylinder with angular velocity
of Mass
and radius
is lowered on a rough fixed wedge of angle
with the horizontal and coefficient of friction
. The cylinder is released at a height of
from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline in
Take , and
The answer is 9.72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Accleleration due to kinetic friction a f = M f = μ g sin θ = 2 3 g 3 = 2 g and g sin θ = 2 g . So, the cylinder will roll until it stops and then start pure rolling.
α ⇒ t 1 = I a f R = R g = g ω 0 R
Now, after this, it will start pure rolling with v 0 = ω 0 = 0
Let a f be the acceleration due to static friction from this stage. ⇒ a n e t = R α Now, g sin θ − a f ⇒ a ⇒ t 2 = I a f R 2 = 2 a f = 2 a f = 3 2 g sin θ = 3 1 g = a n e t 2 s = g sin θ 2 × 3 R ⋅ 3 = 6 g R
∴ t = t 1 + t 2 = g w 0 R + 6 g R
BTW:This question is there in Cengage Textbook