The death star's ratio

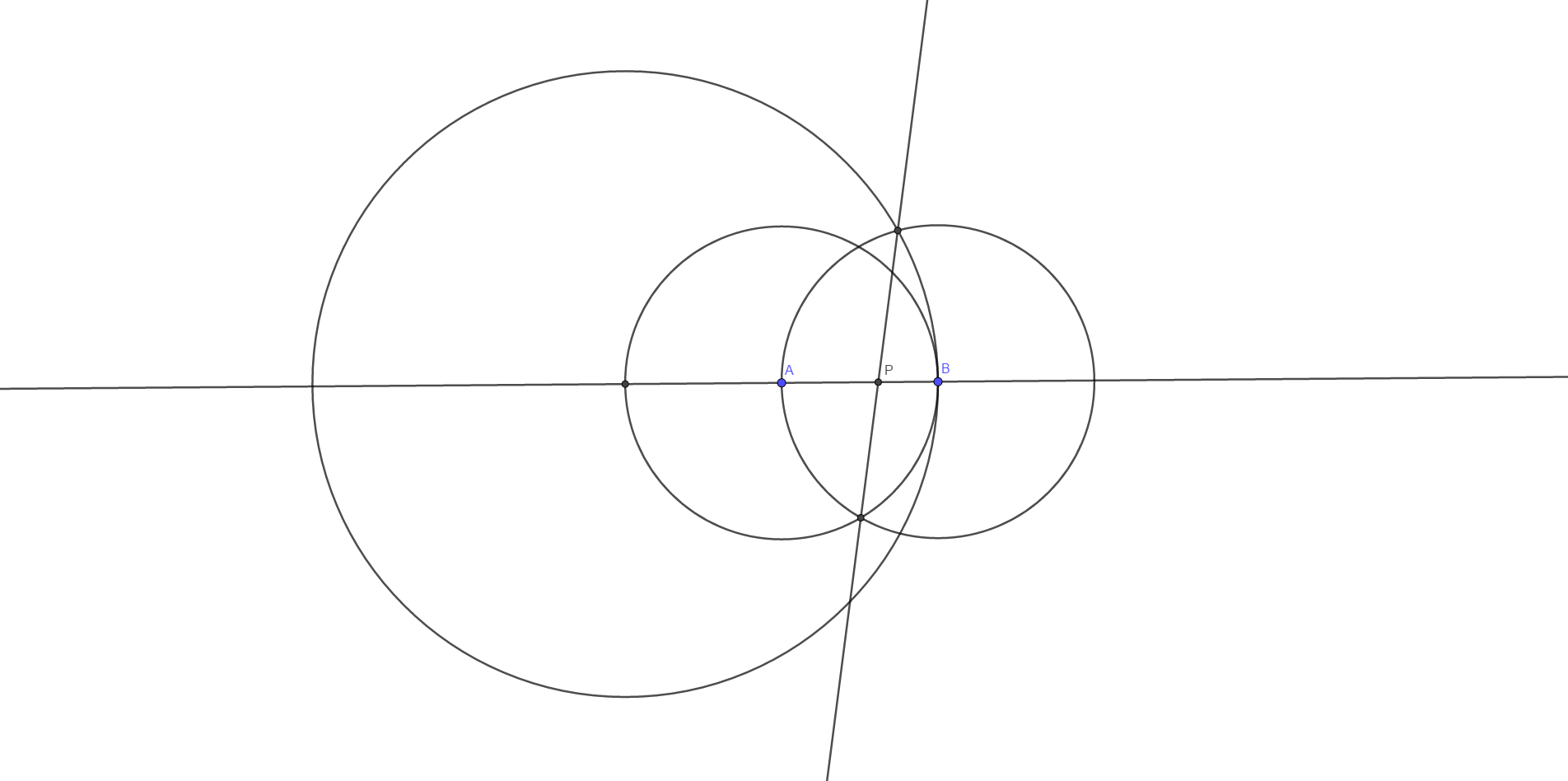
Let $D$ be the center of the big circle, $C$ be the other point of intersection between circle $D$ and line $AB$ , $G$ be the point of intersection of the line and circle D and circle $B$ , and $H$ be the point of intersection of the line and circle $A$ and circle $B$ . Construct triangles $\triangle BCG$ and $\triangle ABH$ . Let $FG$ be the altitude of $\triangle BCG$ and let $EH$ be the altitude of $\triangle ABH$ . Finally, let $r = AB$ .

Since $\triangle BCG$ is inscribed in circle $D$ with $BC$ as its diameter, $\angle BGC$ is a right angle. Since the radius of circle $C$ is equivalent to the diameter of circle $A$ , the diameter $BC = 4r$ . Since $BG = AB = r$ , by Pythagorean's Theorem $CG = \sqrt{BC^2 - BG^2} = \sqrt{(4r)^2 - r^2} = \sqrt{15}r$ . We also have that $\triangle BCG \sim \triangle BGF$ by AA similarity, so $BF = \frac{BG^2}{BC} = \frac{r^2}{4r} = \frac{1}{4}r$ and $FG = \frac{BG \cdot CG}{BC} = \frac{r \cdot \sqrt{15}r}{4r} = \frac{\sqrt{15}}{4}r$ .

Since $AB = BH = AH = r$ by the radii of congruent circles, $\triangle ABH$ is an equilateral triangle, and $BE = \frac{1}{2}r$ and $EH = \frac{\sqrt{3}}{2}r$ .

Setting $B$ as the origin, the coordinates for $G$ are $(-\frac{1}{4}r, \frac{\sqrt{15}}{4}r)$ , the coordinates for $H$ are $(-\frac{1}{2}r, \frac{\sqrt{3}}{2}r)$ , and the coordinates for $P$ are $(-\frac{17}{\pi}, 0)$ . The slope between $G$ and $H$ comes to $m = \sqrt{15} + 2\sqrt{3}$ , and its equation of the line through $G$ and $H$ is $y - \frac{\sqrt{15}}{4}r = (\sqrt{15} + 2\sqrt{3})(x + \frac{1}{4}r)$ . But since $P$ is on this line, we can substitute $x = -\frac{17}{\pi}$ and $y = 0$ to obtain $-\frac{\sqrt{15}}{4}r = (\sqrt{15} + 2\sqrt{3})(-\frac{17}{\pi} + \frac{1}{4}r)$ , which solves to $r = \frac{51 + 17\sqrt{5}}{2\pi}$ .

Since $AP = AB - PB$ , $AP = \frac{51 + 17\sqrt{5}}{2\pi} - \frac{17}{\pi}$ $=$ $\frac{17 + 17\sqrt{5}}{2\pi} \approx \boxed{8.755615652}$ .