The △ prefers to live in colors!
The triangle shown below consists of four small triangles of equal area. If each of the four small triangles are to be filled with one of the four colors (red, green, blue and yellow), such that no two adjacent triangles can have the same color, then find the number of possible combinations.
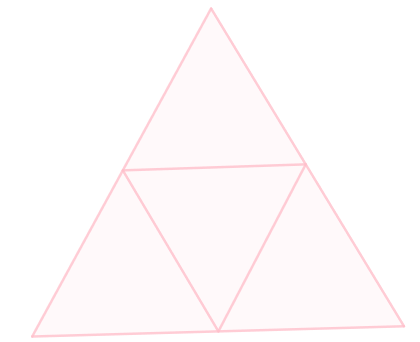
Details and Assumption:
- Each of the four small triangles are to be considered distinct.
- Adjacent triangles are those which have a common edge.
The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
( @Shreyansh Mukhopadhyay also please remove the word "primary" from the question as there are 3 primary colours, not 4)
Nice approach. +1! I wonder what if the problem allows rotation of the triangle on the plane, and asks number of distinct coloring.
We note that the outer three triangles can be filled with any of the four colors. Therefore, there are 4 3 = 6 4 ways of filling them. If the outer triangles are filled with n different colors. where n = 1 , 2 , 3 , then the number of ways to filled the three outer triangles is N o ( n ) = N c ( n ) N p ( n ) , where N c ( n ) = ( n 4 ) is the number of ways to choose n colors and N p ( n ) is the number of ways to permute the n colors among the three triangles. Then, we have:
n 1 2 3 : : : : N c ( n ) 4 6 4 × × × × N p ( n ) 1 6 6 = = = = N o ( n ) 4 3 6 2 4 6 4
The middle triangle however must be filled with a color different from that of any of the three outer triangles. Therefore, the number of ways to fill the middle triangle is N m ( n ) = 4 − n . And the total number of ways of filling the four triangles is given by:
n 1 2 3 : : : : N o ( n ) 4 3 6 2 4 × × × × N m ( n ) 3 2 1 = = = = N ( n ) 1 2 7 2 2 4 1 0 8
Sir, I did the same like @Stephen Mellor , but I have the same question as @Mayank Chaturvedi , what will be the answer when rotations are allowed and we need distinct colorings? Thanks! BTW, nice solution!
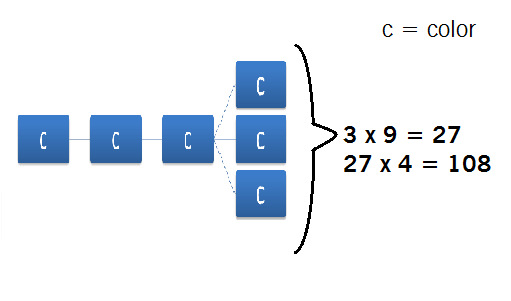
First, assign a colour to the middle triangle (which can be done in 4 ways).
Then, for each of the 3 triangles in the corners, they can be any one of the 3 remaining colours (independently of each other).
Therefore, there are 4 × 3 × 3 × 3 = 1 0 8 ways.