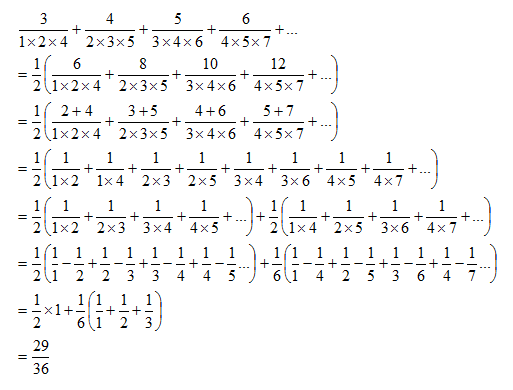The denominator isn't consecutive
1 × 2 × 4 3 + 2 × 3 × 5 4 + 3 × 4 × 6 5 + …
If the above summation can be expressed as b a where a , b are co-prime natural numbers, find a + b .
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Just the common method of partial fractions. f ( n ) = 1 ∑ ∞ n ∗ ( n + 1 ) ∗ ( n + 3 ) n + 2 ∴ n ∗ ( n + 1 ) ∗ ( n + 3 ) n + 2 = n A + n + 1 B + n + 3 C S o l v i n g , n ∗ ( n + 1 ) ∗ ( n + 3 ) n + 2 = 3 2 ∗ n 1 − 2 1 ∗ n + 1 1 − 6 1 ∗ n + 3 1 ∴ f ( n ) = 1 ∑ ∞ { 3 2 ∗ n 1 − 2 1 ∗ n + 1 1 − 6 1 ∗ n + 3 1 } ∴ f ( n ) = 3 2 ∗ 1 ∑ 3 n 1 + 3 2 ∗ 1 ∑ ∞ n + 3 1 − 2 1 ∗ s u m 1 2 n + 1 1 − 2 1 ∗ 1 ∑ ∞ n + 1 1 − 6 1 ∗ 1 ∑ ∞ n + 3 1 3 2 ∗ ( 1 1 + 2 1 + 3 1 ) − 2 1 ∗ ( 2 1 + 3 1 ) + 0 + 0 + . . . 1 8 2 2 − 1 2 5 = 3 6 2 9 . a + b = 2 9 + 3 6 = 6 5 .
Note: The first term 'n' to become 'n+3' needs to move 3 steps so limit 1 to 3. Similarly the second term, to move from 'n+1' to 'n+3' needs to move 2 steps so limit 1 to 2. Since the limit is infinity, all end at infinity. If the limit was say L, term 'n' would end at L - 3, and 'n+1' would end at L-2.
General Term Of The Series Is
T = r+2 / r(r+1)(r+3)
T = 1/2 (r+1+r+3/r(r+1)(r+3)
T = 1/2( 1/r(r+3) + 1/r(r+1) )
We Break Down Series Into Two Telescoping Series
T2 = 1/r(r+1)
Its A Very Very Trivial Telescoping Series
T2 = 1/1 - 1/2 + 1/2 -1/3 + 1/3 -1/4.........
as limit is tending towards infinity so we T2 = 1
Main Thing Is To Evaluate T1 = 1/r(r+3)
Now We Use A Good Trick Here
T1 = 1/3 (1/r - 1/r+1) + 1/3(1/r+1 - 1/r+2) + 1/3(1/r+2-1/r+3)
These Three All Are Telescoping Series Individually
The Sum Evaluates To
T1 = 1/3 (1+1/2+1/3)
Final Sum => 1/2(T1+T2) = 29/36
I Thought Of This Trick While Solving This Problem Only !! Keep Posting
Never thought this way !! I liked your thinking.
did exactly the same wy , thought of adding nd subtracting too ... :) was thinking of uploading it myself :P
1 × 2 × 4 3 + 2 × 3 × 5 4 + 3 × 4 × 6 5 + . . . = n = 3 ∑ ∞ ( n − 2 ) ( n − 1 ) ( n + 1 ) n = n = 3 ∑ ∞ 6 n − 1 2 4 − 6 n − 6 3 − 6 n + 6 1 = 6 4 − 1 2 3 − 2 4 1 + 1 2 4 − 1 8 3 − 3 0 1 + 1 8 4 − 2 4 3 − 3 6 1 + 2 4 4 . . . = 6 4 + 1 2 1 + 1 8 1 = 3 6 2 4 + 3 + 2 = 3 6 2 9 2 9 + 3 6 = 6 5
Moderator note:
It's better to explain how you got R H S for your second line.
Try to put parenthesis into the your third line to make the distinction between each term clearer so that readers will know that it is a telescoping sum.