The Diagonal of a Square
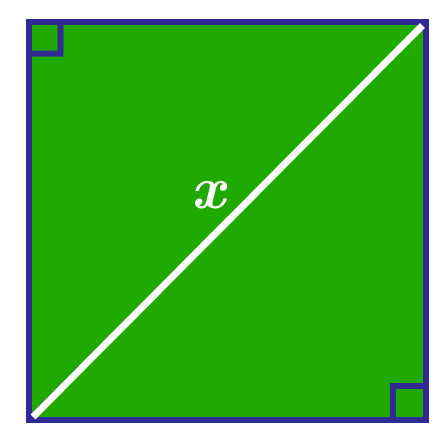
The above shows a square with area 18. What is the length of the diagonal x ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Relevant wiki: Area of Figures
A r e a o f s q u a r e = d 2 / 2 ( w h e r e d i a g o n a l " d " i s g i v e n ) d 2 / 2 = 1 8 = > d 2 = 3 6 t h e r e f o r e d = 6 w h i c h i s t h e r e q u i r e d r e s u l t .
d 2 = 1 8
d = 3 ∗ 2 . 5
x = 2 . 5 ∗ d = 3 ∗ 2 = 6
I came up with about 5.9... depends on how one rounds the solution...
A = s 2
s = A
x = s 2 = 2 A = 2 × 1 8 = 3 6 = 6
We know that the are of a square is a^2 Hence , a=18^1/2 So a^2+a^2=x^2 18+18=x^2 36=x^2 6=x
Area of triangle=1/2 [diagonal]^2
Direct way: consider the four right triangles the interesecting diagonals make. 2 4 ⋅ ( 2 x ) 2 = 1 8
x 2 = 3 6 ⇒ x = 6
Relevant wiki: Pythagorean Theorem
A = s 2 = 1 8
x = s 2 + s 2 = 2 s 2
but: s 2 = 1 8
now we substitute
x = 2 ( 1 8 ) = 3 6 = 6