The disphenoid
Find the closed form of the volume of the disphenoid whose edge lengths are the roots of the polynomial above.
GIve your answer to 3 decimal places.
Definition : A disphenoid is a non-regular tetrahedron whose faces have the same perimeter/area, and thus consist of congruent triangles.
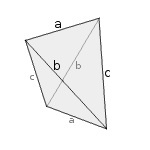 Disphenoid
Disphenoid
Try this easier problem.
The answer is 10.544.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A disphenoid is a non regular triangular pyramid whose faces (including the base) consist of congruent triangles.
The formula for the volume V of disphenoid given its edge lengths a , b , and c is:
V = 7 2 ( a 2 + b 2 − c 2 ) ( a 2 − b 2 + c 2 ) ( − a 2 + b 2 + c 2 )
However, this demands the values of the edge lengths to be known.
A more creative alternative to that would be using Heron's Formula, Newton's Sums, and this relationship
1 6 A 2 R 2 = ( a b c ) 2 + 9 V 2
where
A = area of each face
R = radius of the sphere circumscribing the disphenoid
V = volume of the disphenoid
To find A , we use Heron's.
A = s ( s − a ) ( s − b ) ( s − c )
which again, demands the knowledge of the values of the side lengths. However, notice that these side lengths are the zeroes of the polynomial P ( x ) . We could use that to our advantage and the formula becomes
A = s ⋅ P ( s )
where s , by the way, is half the negative of the coefficient of x 2 . (Do you see why?)
For that we get A = 1 6 2 0 9 1 .
Now, the formula for the circumradius is
R = 8 a 2 + b 2 + c 2
which we can obtain using Newton's sums.
From that, we get,
a 2 + b 2 + c 2 = 1 7 ( 1 7 ) − 2 ( 9 3 )
a 2 + b 2 + c 2 = 1 0 3
So, we get R = 8 1 0 3 .
Now, we're all set to find the volume!
V 2 = 9 1 6 A 2 R 2 − ( a b c ) 2
Substituting the values, we get
V 2 = 7 2 8 0 0 5
and V = 1 0 . 5 4 4 .
Well, you can do this the "boring" way: determining the roots of the polynomial then proceeding to substitution. But I recommend otherwise!