The chase is on!

A dog sees a rabbit running in a straight line across an open field and gives chase in a rectangular coordinate system. Assume that:

1. The rabbit is initially at the origin and the dog is initially at the point from where it first spots the rabbit.
2. The rabbit runs up the $y$ -axis and the dog always runs straight for the rabbit .
3. The dog runs twice as fast as the rabbit. (their speeds are constant)

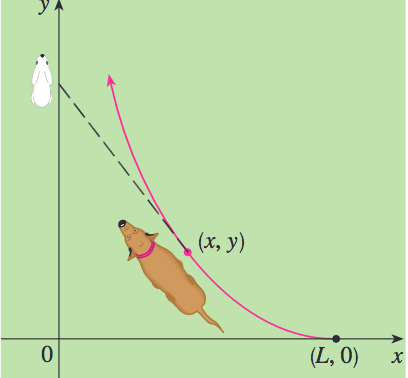
As shown in figure above, the dog starts at the coordinates $(L, 0)$ and all the assumptions are satisfied. If the velocity of the dog in the upward direction is initially zero , find out whether the dog will ever catch the rabbit. If it succeeds, then at what point in the cartesian plane will the chase end?

If the dog never catches the rabbit, submit your answer as $-1$ , else, if the $y$ -coordinate of the dog's final position is of the form $\frac{e^{C - 5} \cdot (6 - A^{2}) \cdot L}{30 - B^{3}}$ , where $A$ , $B$ and $C$ are non-negative integers , submit your answer as the $L^{2}$ norm of the vector: $A\hat{i} + B\hat{j} + C\hat{k}$ .

Courtesy: Stewart Calculus Early Transcendentals Sixth Edition