The Dog's Span II
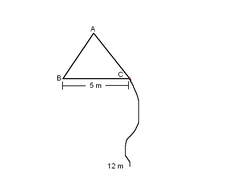 A dog is tied on a triangular pillar with each side measuring 5 meters in the middle on an unfenced lot with infinite area. If the chain is 12 m long, what is the total span of area (in square meters) that the dog can reach? Assume the dog's size to be infinitesimal, and that the chain is not elastic.
A dog is tied on a triangular pillar with each side measuring 5 meters in the middle on an unfenced lot with infinite area. If the chain is 12 m long, what is the total span of area (in square meters) that the dog can reach? Assume the dog's size to be infinitesimal, and that the chain is not elastic.
Express your answer as floor where A is the total span of area (in square meters) that the dog can reach.
Still can't get enough? Try this one.
The answer is 436.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Now we have to determine the area formed by the triangle SAC. S is on the cercle of center C and radius 7 so SC=7, S is also on the cercle of center A and radius 7, so SA=7. Therefore SAC is isosceles. Therefore (SZ) is the perpendicular bisector of segment [AC]. Therefore using the Pythagorean theorem : S Z = S C 2 − Z C 2 = 7 2 − 2 . 5 2 = 4 2 . 7 5
Thus, A y e l l o w = 2 A C × S Z = 2 5 × 4 2 . 7 5 =16.346
Now for the green angular sectors. We have to find the angle E A S . E A C + C A B = 1 8 0 S o , E A C = 1 2 0 Z A S = cos − 1 ( A S A Z ) = cos − 1 ( 7 2 . 5 ) T h e r e f o r e , E A S = 1 2 0 − cos − 1 ( 7 2 . 5 ) ≃ 5 0 . 9 2 5 T h e n , A g r e e n = 2 × 3 6 0 π × 7 2 × 5 0 . 9 2 5 ≃ 1 3 . 8 6 3 π F i n a l l y A t o t a l = 1 2 0 π + 1 3 . 8 6 3 π + 1 6 . 3 4 6 = 4 3 6 . 8 8 T h e a n s w e r i s 4 3 6 .