The Dog's Span I
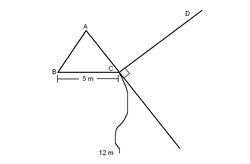 A dog is tied on a triangular pillar with each side measuring 5 meters. The pillar is attached to the corner of a perpendicular fence such that the side of the pillar farthest from where the dog is tied is perpendicular to the fence nearby. If the chain is 12 m long, what is the total span of area (in square meters) that the dog can reach? Assume the dog's size to be infinitesimal, and that the chain is not elastic. Also assume that the dog cannot pass through the point attaching the pillar to the fence.
A dog is tied on a triangular pillar with each side measuring 5 meters. The pillar is attached to the corner of a perpendicular fence such that the side of the pillar farthest from where the dog is tied is perpendicular to the fence nearby. If the chain is 12 m long, what is the total span of area (in square meters) that the dog can reach? Assume the dog's size to be infinitesimal, and that the chain is not elastic. Also assume that the dog cannot pass through the point attaching the pillar to the fence.
The total area can be expressed in the mixed fraction form , where , , and are all positive integers with and coprime. Express your answer in the form .
Can't get enough? Try this.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The maximum area that can be reached by the dog can be obtained by stretching its chain to its maximum distance from the point where it is tied. Since the chain is not elastic, then it will form a circular area around the point where it is tied (as is shown in the red region of the figure above).
The area is found using A = 2 θ r 2 . In this case, the angle θ is obtained by determining the exterior angles of the triangle. Since it is an equilateral triangle, then the angle is found to be 3 2 π . Also, r = 1 2 in this case.
When the dog will try to reach another side of the pillar, its reach will decrease since 5m of its chain is restricted by the first side of the pillar. Thus, the circular area formed will have a radius r = 7 as is shown in the blue region of the figure above.
Can the dog still reach the third side of the pillar? Yes. Since the free chain is 7m long, it can still reach the third side and reach a circular area of r = 2 as is shown in the green region of the figure above.
The total area is then
A t o t a l = 3 1 π ( 1 2 2 + 7 2 + 2 2 ) = 3 1 9 7 π
= 6 5 3 2 π
With this answer, we find that a + b + c equals to 7 0 .
I highly suggest you try this problem too.