The Effect of Scaling on Gravitational Force
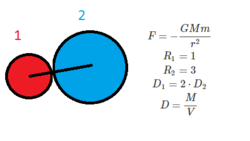 Two solid metal balls are placed in contact with each other. The first ball is made of a material twice as dense as the second ball; the first ball has a radius of 1, the second has a radius of 3. The gravitational force between them is
. The balls are somehow enlarged so that they gain mass proportional to their respective densities (density is conserved) and ball one's radius is twice as large as it was and ball two's radius is five times as large as it was. What is the new force relative to
?
Two solid metal balls are placed in contact with each other. The first ball is made of a material twice as dense as the second ball; the first ball has a radius of 1, the second has a radius of 3. The gravitational force between them is
. The balls are somehow enlarged so that they gain mass proportional to their respective densities (density is conserved) and ball one's radius is twice as large as it was and ball two's radius is five times as large as it was. What is the new force relative to
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Careful reading of the question shows that the distance between the centres of the spheres increases from (1+3) to (2+15), in other words by a factor of 4 1 7 .
Since the mass of a sphere is proportional to the cube of its radius, the masses of the spheres increase by factors of 8 and 125, so their product increases by a factor of 1000.
Looking at the formula for F we can see that it will be changed by a factor
( 1 7 4 ) 2 × 1 0 0 0 ≈ 5 5 . 3 6