The Egyptian Pharaoh

$\begin{array}{c}& A & B & C & D & E \\ \times & & & & & 4 \\ \hline & E & D & C & B & A \end{array}$

1. Find A : Let us start with $A$ of $\overline{ABCDE}$ . Since $A\times 4 = E < 10$ , $A$ has to be either $1$ or $2$ . We note that the product $\overline{EDCBA}$ ends with $A$ . Since a multiple of $4$ must be even $A \ne 1$ and must be $\boxed{A=2}$ .
2. Find E : Now we note that $E$ in the product can either be $8$ or $9$ . If $E=9$ , then $E\times 4 = 36$ , and $A$ in the product would be $6$ , which is incorrect. Therefore, $\boxed{E=8}$ , then $8 \times 4 = 32$ .
3. Find B : From $\overline{AB} \times 4 = \overline{ED} - c_3$ , where $c_3 = 0,1,2,3$ is the carried-forward, we note that $B \times 4 < 10$ , else $E = 9$ , which is unacceptable. Therefore, $B = 1$ or $2$ . From $D \times 4 + c_1 = 10c_2 + B$ , we note that $B$ is odd, because $4D$ is even and $c_1 = 3$ , which is odd. Therefore, $\boxed{B=1}$ .
4. Find D : Therefore, $4D+3 = 10c_2 + B = 10c_2 + 1$ . This means that $4D = 8$ or $28$ or $D = 2$ or $7$ , but $D \ne A = 2$ , hence $\boxed{D = 7}$ .
5. Find C : Now $4(10B+C) + c_2 = 4C + 43 = 10D+C = 70+C$ , then we have $3C = 27\quad \Rightarrow \boxed{C=9}$ .

Therefore, $\overline{ABCDE} = \boxed{21978}$

Given: ABCDE x 4 = EDCBA

The answer is: 21978 x 4 = 87912

But rather than just give you the answer, here's how I figured it out. First, it is obvious that A must be an even number, because we are multiplying by 4 (an even number). The last digit will therefore be even. It can't be 0, because that would make ABCDE a four-digit number. It can't be more than 2, because that would result in a six-digit answer. So A = 2.

2BCDE x 4 = EDCB2

So what can E be? The choices are E = {3, 8} because 3 x 4 = 12 and 8 x 4 = 32. But a value of 3 doesn't work in the result (3????) because it is too small.

2BCD8 x 4 = 8DCB2

Since the final number is 8 and we have 2 x 4, that means there is no carry from the prior multiplication (4 x B + carry). So B can't be anything higher than 1, possibly 0.

Looking at the other side of the equation, we have 4D + 3 = (a number ending in 0 or 1). In other words, 4D must end in 7 or 8. Obviously only 8 works, because 4 is an even number. Working forward again, that means B = 1.

21CD8 x 4 = 8DC12

So what values of 4D result in a number ending 8? 4 x 2 = 8, 4 x 7 = 28. Now 2 is already taken and the problem said the digits were unique. So D = 7.

21C78 x 4 = 87C12

Finally, we have a carry of 3 (from 28 + 3 = 31). And when we calculate 4C + 3 it must also result in a carry of 3 and a last digit of C. In other words: 4C + 3 = 30 + C

This is easy to solve: 3C = 27 C = 9

Thus the final answer is: 21978 x 4 = 87912

A must be less than 10 so that the number stays 5 digit. There can be two values for A, 1 and 2. But since the number is multiplied by 4 it is even. So A is 2.

E can be 8 or 9. E x 4 should have 2 in ones digit. 9 x 4 is 36, 8 x 4 is 32. E now is 8.

Next, B can be 0,1,2. D x 4 + 3 gives an odd number. So B is equal to 1.

D can be 2 or 7. Since 2 x 4 + 3 is 11 and 7 x 4 + 3 is 31 which both result to 1 in the ones digit. But B x 4 ranges from 4 to 9 so we cant have 2 for D. Therefore D is 7.

C x 4 + 3 should be 30 to 39 so that B x 4 + 3 = 7 = D. C now is from 7 to 9. 7 x 4 + 3 is 31, 8 x 4 + 3 is 35, 9 x 4 + 3 is 39. C x 4 + 3 should have C in its ones digit. So C now is 9.

The number is 21978..

Okay, so we have $\overline{ABCDE}*4 = \overline{EDCBA}$ .

Since $\overline{EDCBA}$ is a multiple of $4$ , it is an even number, and thus $A$ must be even. Furthermore, since $\overline{EDCBA}$ has $5$ digits, $\overline{ABCDE}$ can be at most $24999$ , for $25000*4 = 100000$ .

Thus, $A$ is either $0$ or $2$ .

Suppose that $A = 0$ ; this gives us $E = 0$ or $E = 5$ , since the only digits that multiplied by $4$ ends in $0$ are $0$ and $5$ . Suppose that $E = 0$ ; then, $\overline{BCD0}*4 = \overline{DCB0}$ . Then, since the greatest value for $\overline{DCB0}$ is 9990, we have that $\overline{BCD0} \leq 2495$ ; thus, $B \leq 2$ . If $B = 0$ , then: $\overline{CD0}*4 = \overline{DC00}$ . Since $\overline{CD0}$ is at most $990$ , then $\overline{DC00} \leq 3960$ , and so $D \leq 3$ . However, since $D0*4$ must end in $00$ , then $D = 0$ , which gives us $\overline{C00}*4 = \overline{C00}$ , which implies that $C$ must be $0$ as well - and we have a solution, $"00000"$ which I don't think that counts... Let's keep going.

If $B = 1$ , we'd have: $\overline{1CD0}*4 = \overline{DC10}$ , which doesn't work because the last two digits of all multiples of four must form a number divisible by $4$ - and $10$ isn't.

If $B = 2$ , then: $\overline{2CD0}*4 = \overline{DC20}$ . Now, we must have $D = 3$ or $D = 8$ , since these are the only digits that when multiplied by $4$ yield a last digit of $2$ . However, since $B = 2$ , then $D = 8$ , for all numbers between $2000$ and $2499$ , when multiplied by $4$ , begin either with $8$ or $9$ .

Then, we have: $\overline{2C80}*4 = \overline{8C20}$ . From previous calculations, we've established that $C \leq 4$ . Let's test this:

$2080*4 = 8320 \neq 8020$

$2180*4 = 8720 \neq 8120$

$2280*4 = 9120 \neq 8220$

$2380*4 = 9520 \neq 8320$

$2480*4 = 9920 \neq 8420$

Thus, this condition does not yield a solution. Let's turn to the other case, where $E = 5$ .

We can write: $\overline{BCD5}*4 = \overline{5DCB0}$ . However, the smallest $5$ -digit number, $50000$ , when divided by four, is $12500$ , which is still a $5$ -digit number. Thus, we must have $A = 2$ .

If $A = 2$ , then we must have either $E = 3$ or $E = 8$ in order for the last digit of $\overline{EBCDA}$ being equal to $2$ , since these are the only digits that when multiplied by $4$ give us a last digit of $2$ . However, since we have $A = 2$ , then $E$ must be equal to $8$ , for any number between $20000$ and $24999$ when multiplied by $4$ begins with either $8$ or $9$ ; we now have: $\overline{2BCD8}*4 = \overline{8DCB2}$ .

The greatest number of the form $\overline{8DCB2}$ is $89992$ , that when divided by four yields $22498$ . This limits the value for $B$ : $B \leq 2$ . Now, if $B = 0$ , then $\overline{8DC02}$ can never be divisible by $4$ since all multiples of $4$ have the number formed by their last two digits also divisible by $4$ . This also occurs if $B = 2$ , but not if $B = 1$ , though - $22$ is not divisible by $4$ , but $12$ is indeed a multiple of $4$ , so it's valid to assume that $B = 1$ .

Now, we have: $\overline{21CD8}*4 = \overline{8DC12}$ . The greatest number that theoretically could be formed is $21998$ ; when multiplied by $4$ , it yields $87992$ .

Now, from the previous calculation, we've established that $D$ is at most $7$ , Thus, we can write $0 \leq D \leq 7$ . $D$ cannot be $0$ , since if it were, then the last digits of $\overline{EBCDA}$ would equal $32$ and not $12$ .

If $D = 1$ , then the last digits of $\overline{EBCDA}$ would be $72$ ; if $D = 2$ , then the last digits of $\overline{EBCDA}$ would be equal to $12$ and match. We'd then have: $\overline{ABCDE} = \overline{21C28}$ ; however, $21000*4 = 84000$ , and so there is no matching $C$ that can overcome the fact that this number, when multiplied by $4$ , would be greater than a number of the type $\overline{82C12}$ .

Moving on, if $D = 3$ , then the last digits of $\overline{EBCDA}$ would be $52$ ; if $D = 4$ , then these would be $92$ ; if $D = 5$ , they'd be equal to $32$ ; if $D = 6$ , they'd be equal to $72$ .

If $D = 7$ , however, then the last digits are $12$ . Then, we have: $\overline{ABCDE} = \overline{21C78}$

When multiplying this number by $4$ , we must again note that $21000*4 = 84000$ , which implies that $C$ must provide a carry value of $3$ on the thousand's place in order for the multiplication to hold. Thus, $C = 8$ or $C = 9$ ; if $C = 8$ is taken, it yields $21878*4 = 87512 \neq 87812$ . We're left with $C = 9$ , and it does hold that $21978*4 = 87912$ . Therefore, $\overline{ABCDE} = 21978$ , and it's the only solution possible.

I discovered a secret, a most marvelous shortcut in which I can determine BA + 9 = AB. But I shall not share it​

40000 A + 4000 B + 400 C + 40 D + 4 E = 10000 E + 1000 D + 100 C + 10 B + A

=> 39999 A + 3990 B + 300 C = 9996 E + 960 D {Better because simplified.}

We know A has to be smallest i.e. 1 or 2. However, with thorough scientific method:

FOR A:=1 TO 9 DO

FOR B:=1 TO 9 DO

FOR C:=1 TO 9 DO

FOR D:=1 TO 9 DO

FOR E:=1 TO 9 DO

Only A B C D E = 21978 is found. Checked 87912 to be correct.

Answer: 21978

I used simple code to solve this; sorry for being so awkward because this is so in the future: 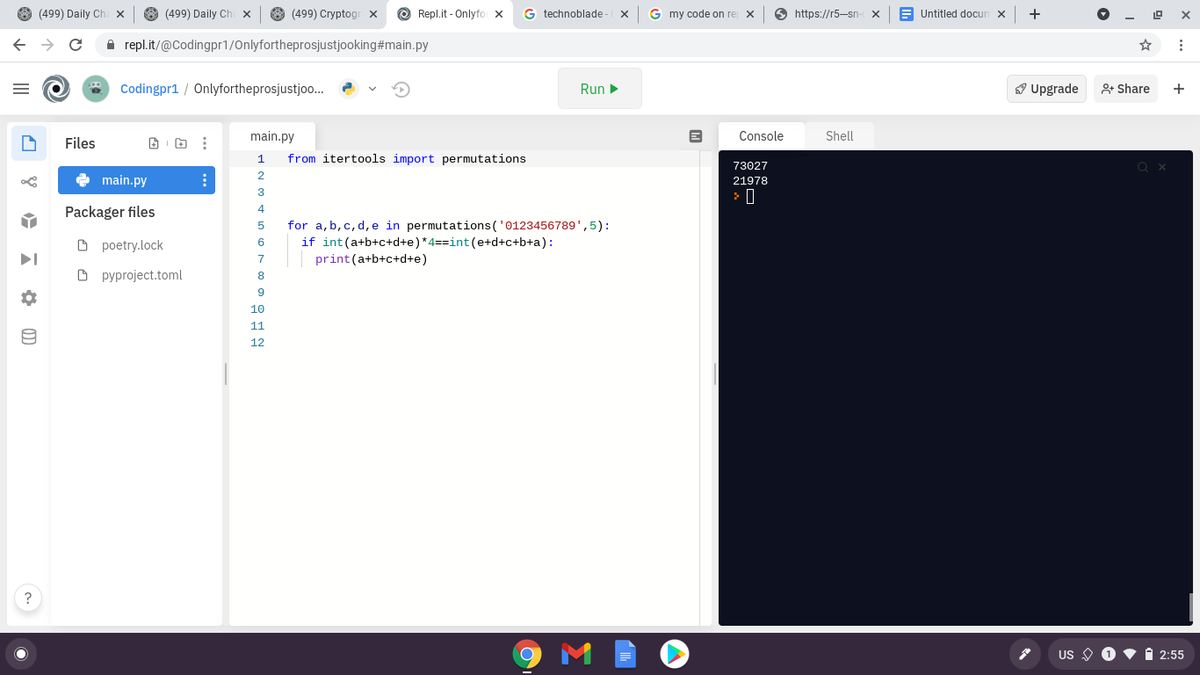Don't mind the 73027 on the top line; that was from a previous output.

It's easy the only main thing is to see A should be less than 3 so, it can be 2 or 1 so, Put u r imagination on...!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def revDigits(n):
    ans = 0
    while n:
        ans = ans*10 + n%10
        n /= 10
    return ans

for i in range(10000, 99999):
    if revDigits(i)==4*i:
        print i

Python

A bit of programming :P