The Ellipse Story
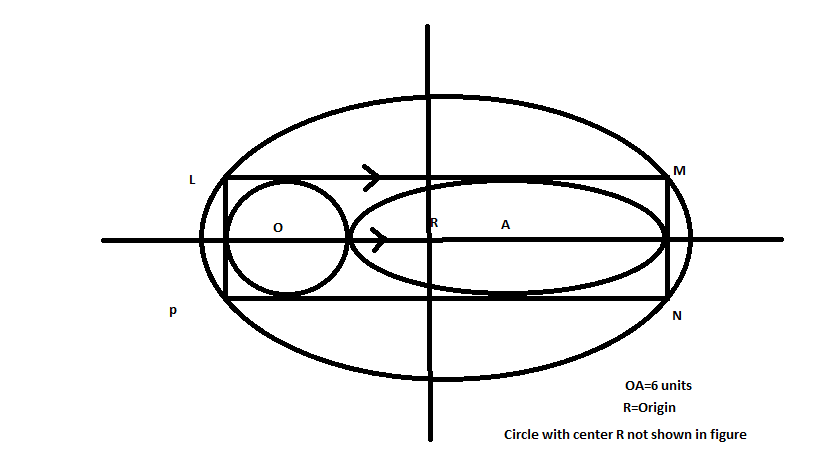
A Circle with center and an ellipse with center are inscribed in a rectangle of maximum possible area that can be inscribed for the ellipse having center at origin R. The area of rectangle of is as shown in figure. A Circle is drawn with center at of radius . Given that a Common Tangent with slope is drawn to the bigger ellipse and the circle with center R. Find .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given that, the distance between smaller circle and ellipse is 6 .
So, the length of the rectangle is
2*6= 12
Given, area of the rectangle= 48
12*breadth =48
Breadth= 4.
Let the equation of bigger ellipse be a 2 x 2 + b 2 y 2 = 1
Given that, the area of the rectangle is maximum.
We know that, if the area of the rectangle is maximum in an ellipse ,
Then ,length= a 2
a= 2 1 2 ; a 2 = 72
Breadth= b 2
b= 2 4 . ; b 2 = 8
Now, equation of tangent ,
For ellipse ⟹ y = m x + a 2 m 2 + b 2
For circle ⟹ y = m x + r ( m 2 + 1 )
Since, it is a common tangent, comparing the constant ,
a 2 m 2 + b 2 = r ( m 2 + 1 )
a 2 m 2 + b 2 = r 2 ( m 2 + 1 )
Given, r= 6
7 2 m 2 + 8 = 3 6 ( m 2 + 1 )
On simplifying,
m 2 = 9 7