The Elliptorus

Calculus Level 5

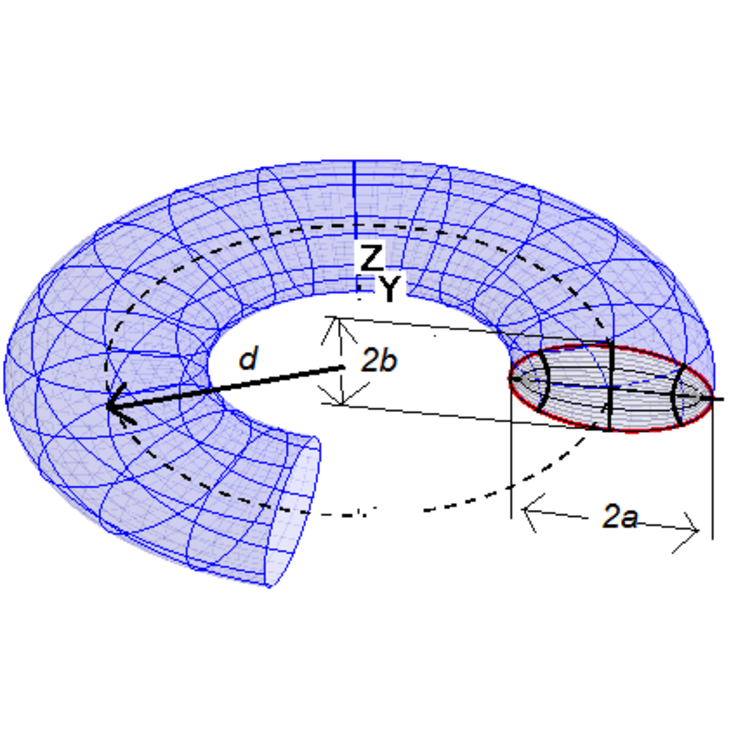Consider the solid above. It's completely filled with a liquid of density ρ = 1.75 × 1 0 3 kg/m 3 \rho = 1.75\times10^3 \text{ kg/m}^3 .

Given that a = 50 cm , b = 30 cm , d = 70 cm a = 50\text{ cm}, b= 30\text{ cm}, d =70 \text{ cm} , the mass of the liquid in kilograms can be expressed as A B π α \dfrac AB \pi^\alpha for coprime positive integers A , B A,B with integer α \alpha , find the value of A + B + α A + B+ \alpha .


The answer is 739.

Kunal Gupta by Kunal Gupta , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Matteo De Zorzi
Oct 27, 2015

It's easy to note that the center of mass of the solid is at a distance D from the center of cordinates( simmetry). In order to have the mass we must find the volume of figure. I'll use Pappo's theorem.. Imagine to move the ellipse in circle of radius D so that the center will move 2πD, the area of the ellipse is πab( it can be shown by simple integration) then the product of the two will be eqaul to the volume of what we are looking for.. Put the value and multiply by density hence results.

1 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...