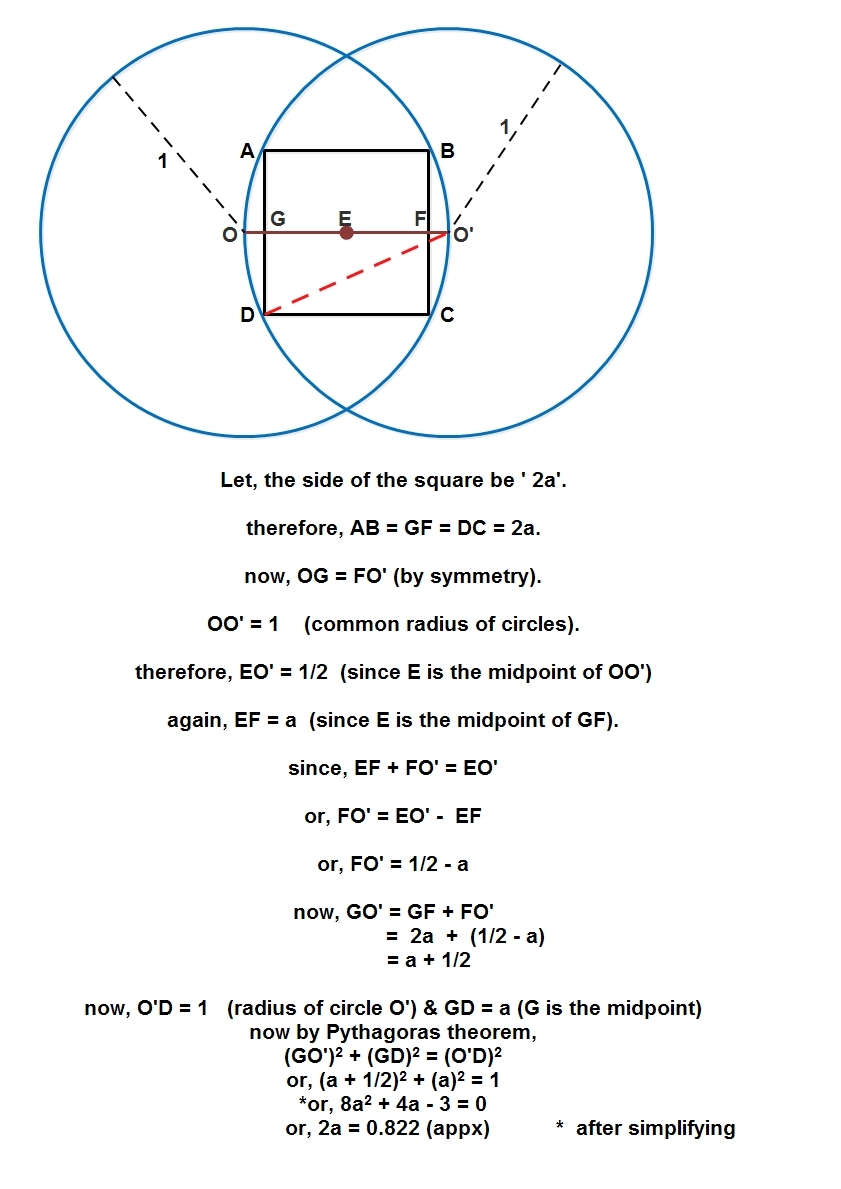
The Enclosed one
The figure above shows two circles , each of radius 1 cm passes through each center. A square is inscribed inside the region enclosed between these two circles. Find the side length of this square (in cm ).
Give your answer to 3 decimal places.
The answer is 0.822.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
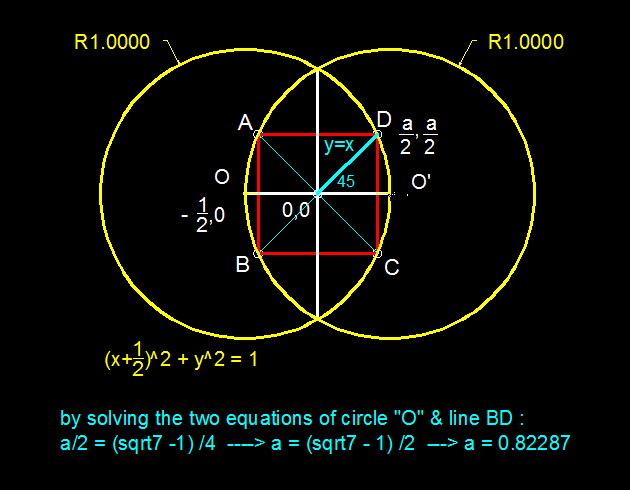
Nice one! But the Diagram needs a little correction...
What is the error in diagram?
circles centers are not in the correct position.. ha ha! ;( just a joke.. but nice solution using CG .cheers!
yes, you are right. I'll correct it.
Now its perfect... Upvoted!
Square with EB as a diagonal is quarter of square ABCD.
Also F is mid point of BC, E of GF and OO'. And BF=EF= say x. OE=EO'=
2
1
.
Using Pythagoras Theorem in right triangle OBF.
O
B
2
=
O
F
2
+
B
F
2
,
⟹
1
2
=
(
2
1
+
x
)
2
+
x
∗
2
.
S
o
l
v
i
n
g
q
u
a
d
r
a
t
i
c
i
n
x
,
x
=
0
.
4
1
1
4
.
B
u
t
B
C
=
2
x
=
0
.
8
2
2
8
.
Log in to reply
Your approach is same as of mine.. only the difference is that you have used the upper portion of the square.. good solution though.. cheers!
nyc approach !
If you want the exact answer without using graphs:
Take the side of the square to be 'a'
BE² = EF² + FB²
BE = √(2*(a/(2))²) = a/(√2)
Triangle BEO has sides BE = a/(√2), B0 = 1 and EO = 0.5
Angle BEO = 90° + 45° = 135°
Using cosine rule on triangle BEO,
1² = 0.5² + (a/(√2))² - 2 * 0.5 * a/(√2) * cos(135)
1 = 1/4 + a²/2 - a/(√2) * - √(2)/ 2
1 = 1/4 + a²/2 + a/2
After some rearranging...
2a² + 2a - 3 = 0
a = (√(7)-1)/2 (= 0.8228...)