The Enveloping Lines Part (a)
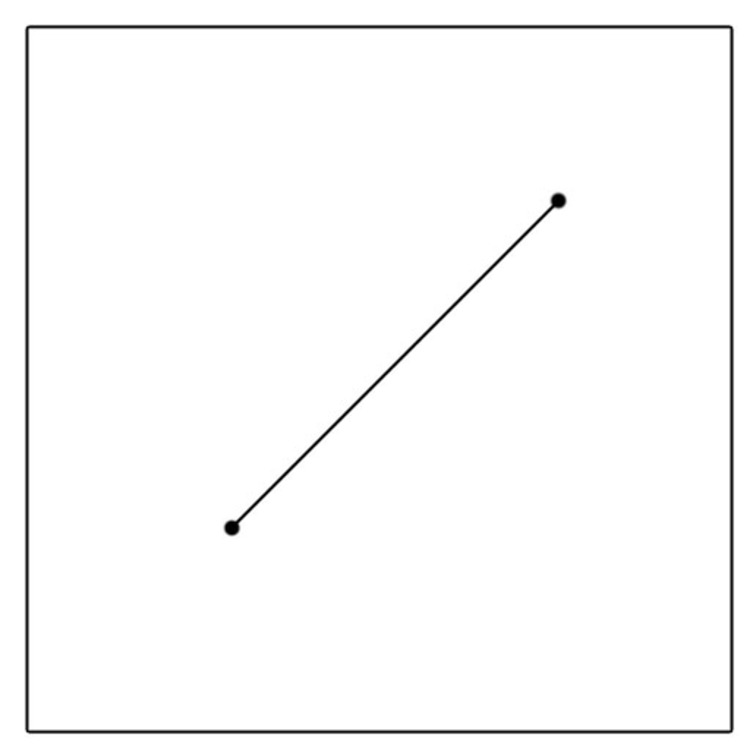2 random points are chosen in a unit square. These points are then linked to form a line such as the one displayed in the picture above.
What is the expected value for the length of the line segment?
Enter your answer to 3 decimal places.
The answer is 0.521.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Given two points ( x , y ) , ( z , w ) in the unit square, the distance between them is ( x − z ) 2 + ( y − w ) 2 . Therefore, the answer is ∫ 0 1 ∫ 0 1 ∫ 0 1 ∫ 0 1 ( x − z ) 2 + ( y − w ) 2 d x d y d z d w ≈ 0 . 5 2 1 .