The Equilateral Triangle Wizardry Part-2
In an e q u i l a t e r a l triangle Δ A B C , there is a point M inside the triangle, such that M A : M B : M C = 3 : 4 : 5 .
Find ∠ A M B in degrees.
(You may need to use the calculator at the end.)
The answer is 133.221.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In response to Alan Enrique Ontiveros Salazar ..Can you plz say me how u derived dat formula through rotation :)
How do you know the formula?
Log in to reply
Derived it from rotations, probably.
Yes, I derived it from rotations.
Log in to reply
@Alan Enrique Ontiveros Salazar Will you please tell me how to solve it by rotations, or please tell me how we approach it by rotations....
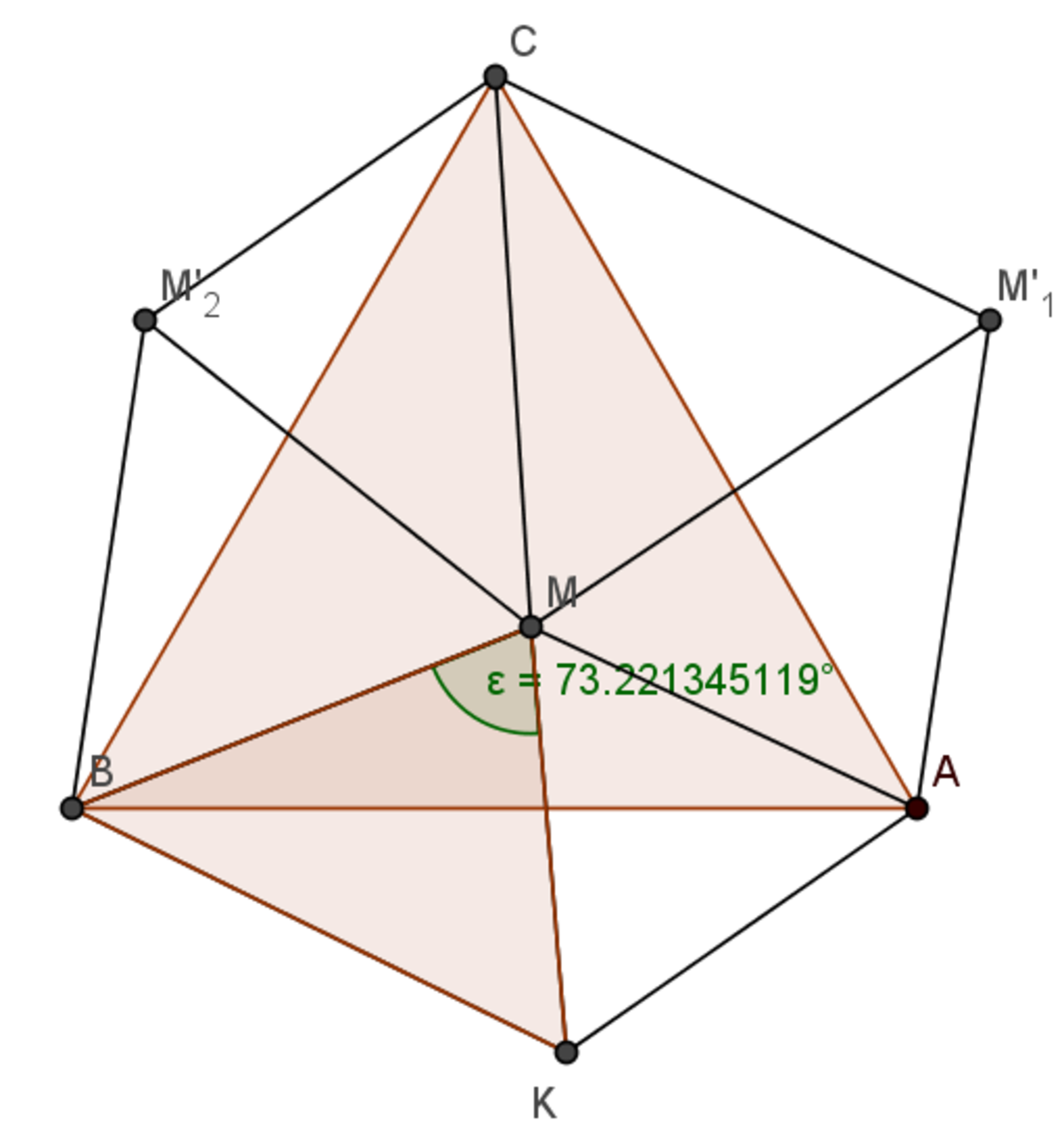
If we make an equilateral △ K M A then △ M B K has side lengths of M A , M B , M C . Then our ∠ A M B = ∠ B M K + 6 0 = 1 3 3 . 2 2 1
We can solve it easily by rotations. But, there is also a formula that gives us the side L of the equilateral triangle knowing a = M A , b = M B and c = M C . That formula is:
L = 2 a 2 + b 2 + c 2 + 3 ( ( 2 a b ) 2 − ( a 2 + b 2 − c 2 ) 2 )
Let a = 3 k , b = 2 k and c = 5 k .
Substituting we get:
L = 6 + 3 3 k
Using Law of Cosines on △ A M B , we get:
cos ∠ A M B = 2 a b a 2 + b 2 − L 2
cos ∠ A M B = 4 3 k 2 7 k 2 − ( 6 + 3 3 ) k 2
c o s ∠ A M B = 1 2 3 − 3 1 1
∠ A M B ≈ 1 3 3 . 2 2 1 °