This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
44 solutions
Moderator note:
Nice use of identifying 2 1 0 = 1 0 2 4 . Slight improvement: 2 9 9 9 > 2 2 0 = ( 2 1 0 ) 2 = 1 0 2 4 2 > 9 9 9 2 .
Just got tricked by the problem's name "Aren't they the same thing?"
What have u done
Wow, I got this right, but I didn't know how! That's incredible!!!! <3
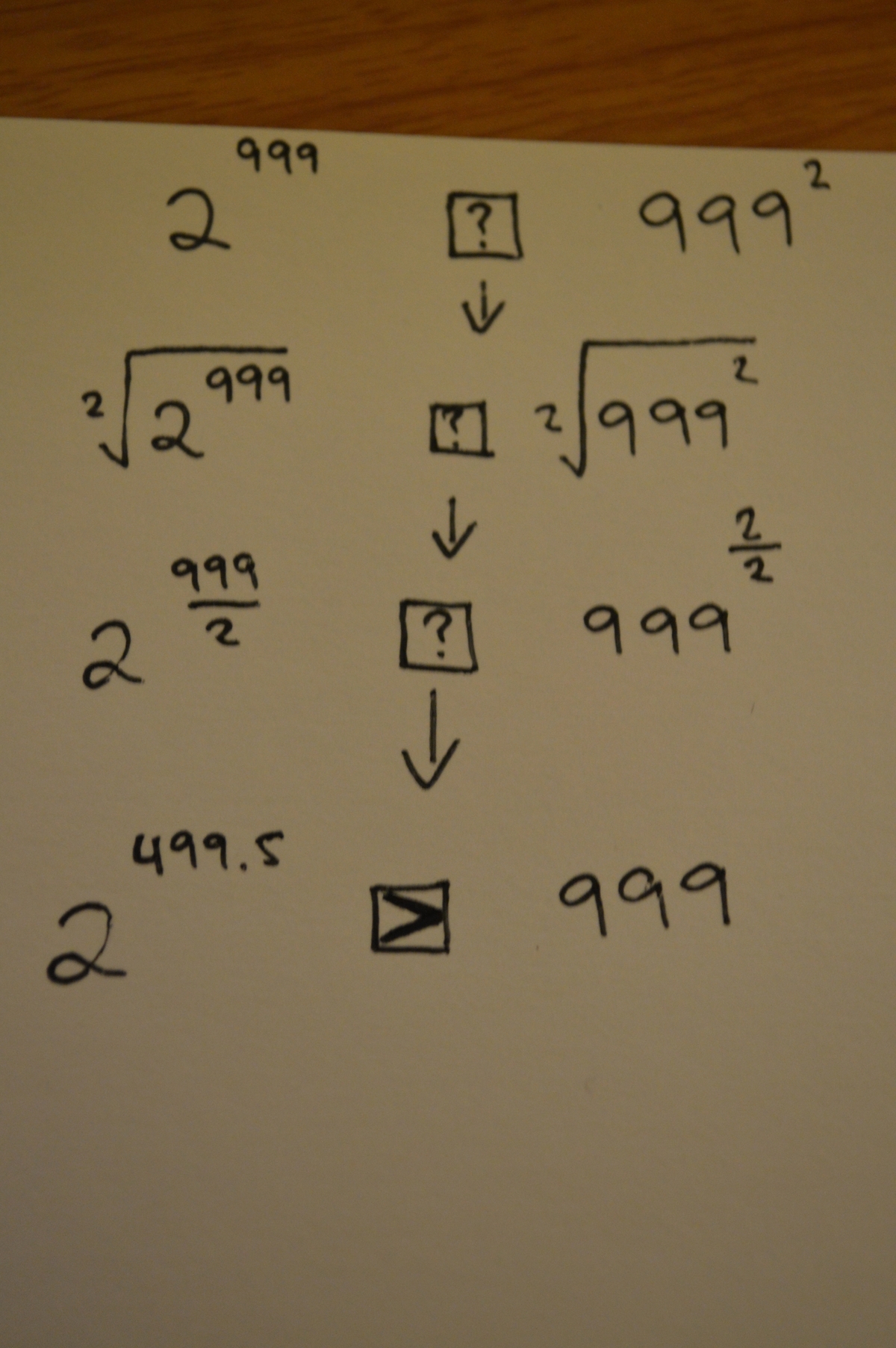
Then you will be able to say (if you have ever powered 2 to anything) that 2^{10} (1024 I believe) itself is larger than 999.
Then 2^{499.5} must be!
Taking logs of both numbers we get 2 9 9 9 ⇒ lo g 2 9 9 9 = 9 9 9 lo g 2 ≈ 1 0 0 0 × 0 . 3 = 3 0 0 9 9 9 2 ⇒ lo g 9 9 9 2 = 2 lo g 9 9 9 ≈ 2 × 3 = 6
It is clear that 2 9 9 9 will be larger than 9 9 9 2 .
Moderator note:
Yes. This is the conventional approach, although you must find know that lo g 2 ≈ 0 . 3 . For clarity, you should mention how you approximated lo g 2 .
(999
)(999)=(6 digit number) .
(2^10)
(2^10)
(2^979)=(1024)
(1024)
(2^479)=(8 digit number)
(2^479).
8 digit number > 6 digit number.
power increases the value very rapidly
such as 9 9 9 2 = 9 9 8 0 0 1
and , 2 2 0 = 1 0 4 8 5 7 6
so, 2 9 9 9 > 9 9 9 2
Since both number base ie, 2 and 999, positive, we can use logarithm test. So clearly, 999ln2 (999x0.3=300 approx) is greater than 2ln999 (approx. 2x3=6) . Hence 2^999 is greater.
This problem can be easily be solved by logic as well as by binomial theorem
Note That: 2^999 = (2^20) (2^979) =(2^10)^2 (2^297)=2^297 (1024)^2 > 1024^2 > 999^2 From the above inequality, obviously that: 2^999 > 999^2.
squaring both terms or 2^999/2 and 999^2/2 becomes 2^449.5 and 999 respectively. Now the question is how many times would you raised up the value of 2 to atleast equal the value 999. Or in eqtn 2^x=999, solving for x= ln(999)/ln2=9.96434 or we can say that 2^10>999.....far less when 2 is raised up to 499.5.
My maths is rather rusty after all these years. I manage to get the answer right but my reasoning might be wrong. I reasoned that 2^9 > 9^2 and so 2^999 must be bigger than 999^2. Correct me if I am wrong.
Ha ha ha.😀😉😏☺️😃😄😐
999^2 would give you a 6 digit number because the digits are always doubled when we square . Then you get 2^14 as 4102 and 2^999 is definitely going to be over 6 digits.
because power increases the value rapidly
1000x1000 is greater than 999^2 and equals 1 million. 32 bit computers cannot address memory beyond 4gb so 2^32 is approx 4 billion. So 2^32 is approx 4000 times greater than 1000^2 therefore 2^999 is hugely bigger than 999^2. Not very mathematical I know but for me was the easiest way to figure it out
Great logic.
[ln(999^2)= 2ln (999)] < [ln(2^999)=999 ln(2)]; Note: 1) ln(999) it's a small number. 2) if ln(x)<ln(y) => x<y
2^999 = 999 * lg2 and lg 2 is between 1 and 2, so that makes it certainly more than 999; 999^2 = 2 * lg 999 and lg 1000 = 3, so lg 999 is certainly less than 3 and that makes it less than 6. Conclusion, 999>6.
Thought this might be useful: the number of digits in the powers of 2 increase when the power ends with 0, 4, 7 e.g. 2^0 = 1(1 digit). 2^4 = 16 (2 digits). 2^7 = 128 (3 digits). 2^10 = 1024 (4 digits) etc. Going by this, there would already be 30 digits in 2^99, and about 300 digits in 2^999. 999^2 on the other hand, = 9^2 * 111^2 = 81 * 12321 which can never be anywhere close to 300 digits
Under speculation with the exponential trend this was an easy question.
Layman's solution... Well, 1000 squared is 1,000,000. 2 to the power of 999 is going to be way more than 1,000,000.
First, I rounded up to make it easy to do in my head, 1000X1000=1,000,000. (6 zeros) 10to 999 would have 999 zeroes, so, even after you divided by 5 to get back to the original 2, there are still WAY more than 6 zeros on the end of the answer??
it can be solved by log also
1000 times 1000 with produce a figure containing 7 digits; so 999 times 999 cannot produce a figure exceeing 7 digits. 2 raised to the power of 999 will result in a figure far exceeding 7 digits.
You just have to use common logic, of course it's 2^999, cause it's the one that at first seems smaller
2^10 = 1024; 2^20 = 1024 x 1024; 900^2 = 810 000; So, 2^20 > 900^2; and 2^999 > 999^2
999 is nearer to 1000 so square of 999 will be less than 2 power 999
 I solved it focusing the problem in the divisors of each number. If we compare the divisors, we can prove that 2^999 is greater than 999^2.
I solved it focusing the problem in the divisors of each number. If we compare the divisors, we can prove that 2^999 is greater than 999^2.
Can be solved by binomial theorem
Obviously that 2^999 is bigger than 999^2. In one case you have 999 calculations of 2 2, while in the other 999^2 you have only one of 999 999.
its not 999999.. it is 999X999
In general,
a b > b a for a< b since 2 < 999, then, 2 9 9 9 > 9 9 9 2
Your statement is wrong. E.g 2^3 > 3 ^2 it completally false.
also incorrect example 2^3=8 and 3^2=9 therefore a^b is not always greater than b^a the other solutions provide the correct deduction not yours
Yes in general Sir but not 100% accurate. What if a= 2 and b=3 or 4?
2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2>999x999
I counted, There was really 999 2x. I was about to write down what 2^999 was, but soon I figured that it would be a 300 digits number.... and gave up.
dude u wrote 2 1089 times...count properly,,,
Log2^999>log999^2, log to the base 2.
Hard but how did you work this out.
exponents get wild really fast, so that's probably bigger than just something squared. :)
You can round it 2^999 ~2^1000 and 999 ^2 is ~1000*1000.
if we go on doubling 2, beyond a point it is huge compared to multiplying 999 only 2 times
Moderator note:
What do you mean "beyond a point"? And how do you prove that it's "huge compared to multiplying 999 only 2 times"?
Can't we use the 'no. of possibilities or cyclicity?
Moderator note:
This is not a solution. What "possibilities or cyclicity" are you referring to?
Moderator note:
Although your inequality is true. You failed to make a connection to the question. Generally, the questions asked you whether X > Y is true or false. But you gave Z > Y instead. You must make another inequality stating that X > Z . Do you see why?
Let's assume 999^2 as 1000^2. We know from simple multiplication that 1000^2 is 1 million. But we also know that even 2^27> 1000000. And it's obvious that 1000^2> 999^2. Meaning 2^999>999^2.
Moderator note:
Poor choice of words. Though I understand what you're trying to say, it's not sound to say that "Let's assume 999^2 as 1000^2". It's like saying "Let's assume pi as 22/7", you would have gotten the wrong answer in this question if you used the same idea.
Actually, the pi question 'Challenge Master' identified is different, and not a good allegory to this question. This question deals with a greater difference in scale which is sufficient to identify the answers given in multiple choice. When there is such a huge difference in scale, rounding would approximate the correct answer better in this case. And it would save time on calculations.
log2 (2^999) = 999
log2 (999^2) = 2log2 (999)
log2 999
2^10 = 1024
let's assume that log2 999 = 9
so 2log2 (999) = 18
999 > 18
so
2^999 > 999^2
Moderator note:
Poor phrasing. You should say that because 2 9 < 1 0 0 0 < 2 1 0 , then lo g 2 9 9 9 is in between 9 and 1 0 .
Do you even need a solution for this ? especially, when there is a calculator.
Moderator note:
You should not depend on calculators all the time. What if the question changed to this: Is 2 9 9 9 , 9 9 9 , 9 9 9 , 9 9 9 bigger than 9 9 9 , 9 9 9 , 9 9 9 , 9 9 9 2 ? Can you solve this with your simple scientific calculator?
(2powe10) = 1024 99 to the power of 1024 obviously greater than 2 power to the 999.
it can be done with simple logic i.e 2^999 will consist 2 ,999 times whereas 999^2 will consist 999 , 2 times so we can easily say that 2^999 is the correct ans.
Moderator note:
Your logic would have failed if we're comparing 1 9 9 9 and 9 9 9 1 . You didn't elaborate on why must 2 999 times is larger then 999 twice?
Knowing properties of exponents and rewriting the fractions using estimates is how I solved it.
To show that 2^999 is larger than 999^2 , simply take log base 2 or log base 999 of both sides.
After completing that, I was left with
999>2log_2(999)
If you understand logs, simply looking at this makes it obvious that the LHS is much larger, but more simplification makes it more clear.
999/2 (~500) > log_2(999)
You know that 500 is larger than log 2 (999), because log 2(1024) is larger than log_2(999) and it is only equal to 10.
999/2 is clearly much larger than 10.
This is an eyeballer when you simplify.
Moderator note:
Yes, logarithm is indeed one way to solve this problem. Though you should be careful with how you phrase it, you should not make the assumption that the proposition is true first. For starters, try to prove by contradiction first: Prove the negation of this inequality is false. That is, using the same approach you mentioned above, prove that 2 9 9 9 ≤ 9 9 9 2 is absurd.
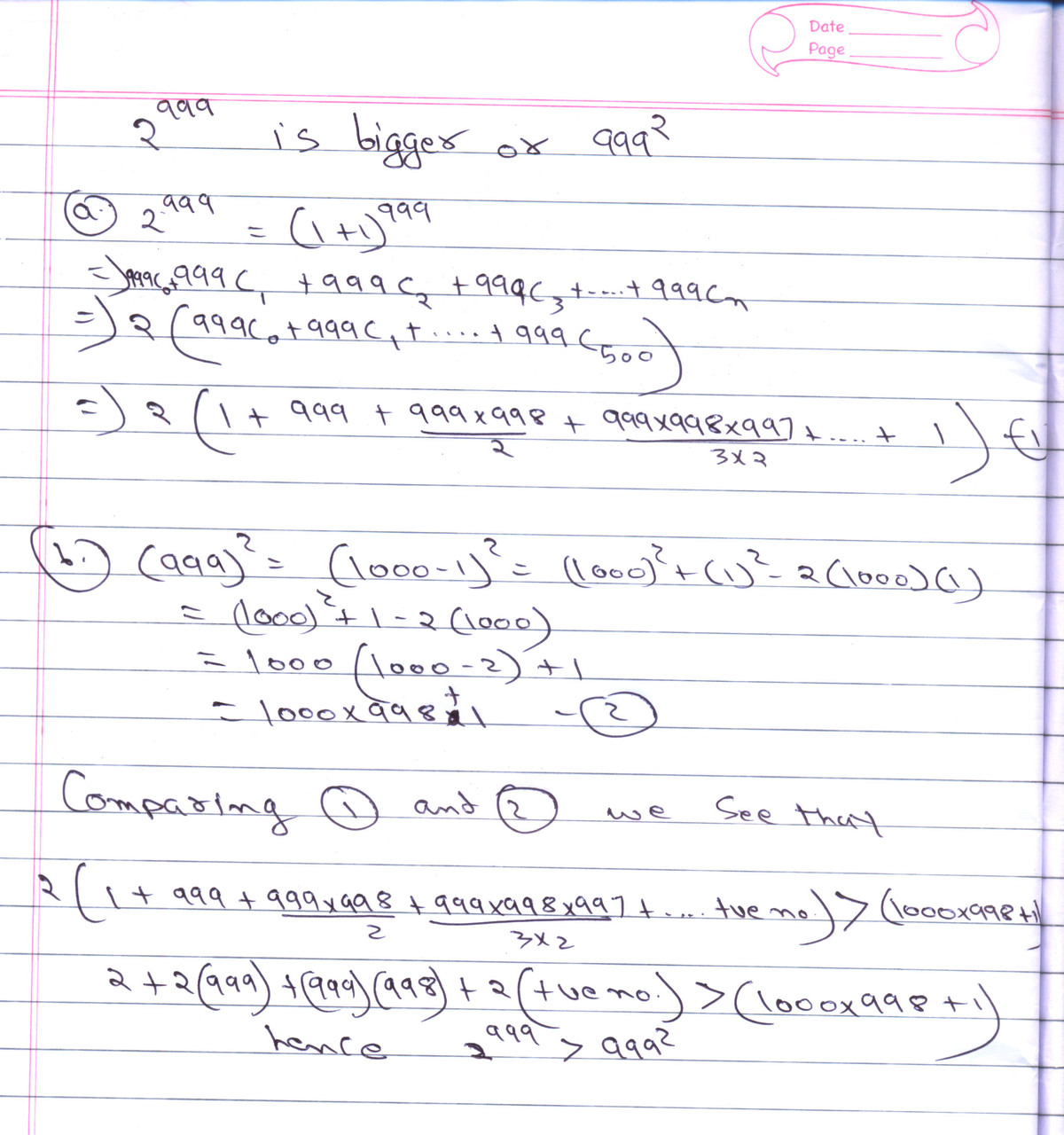

2 9 9 9 = 2 9 7 9 × 2 2 0 = 2 9 7 9 × 1 0 2 4 2 > 1 0 2 4 2 > 9 9 9 2 .