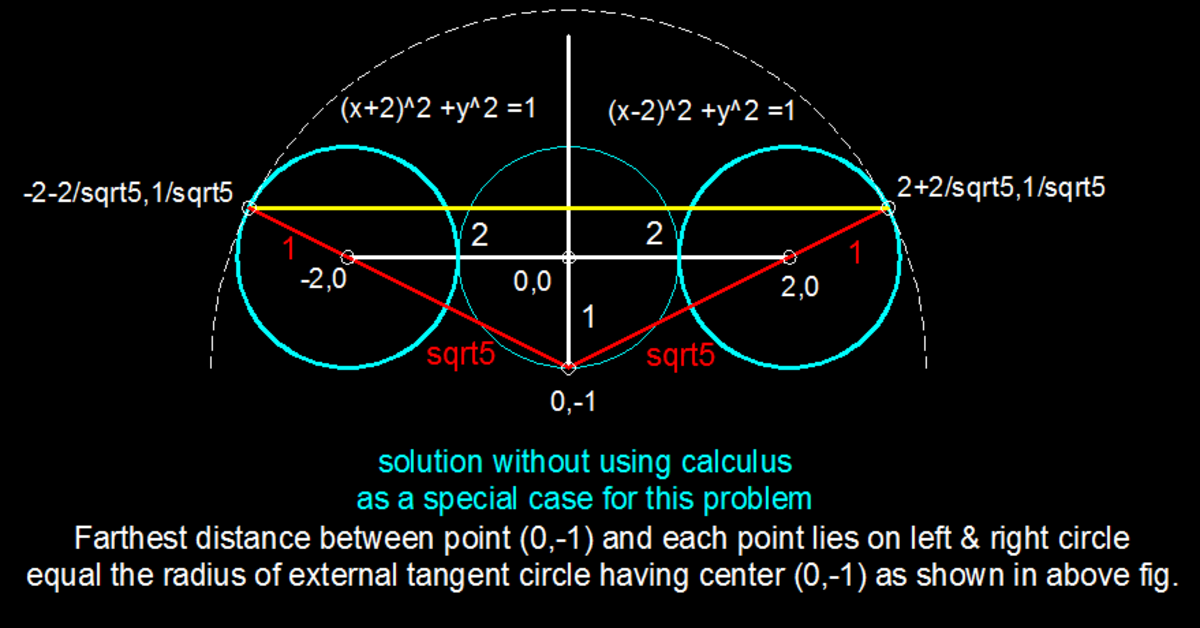
The Farthest Point

Geometry Level 5

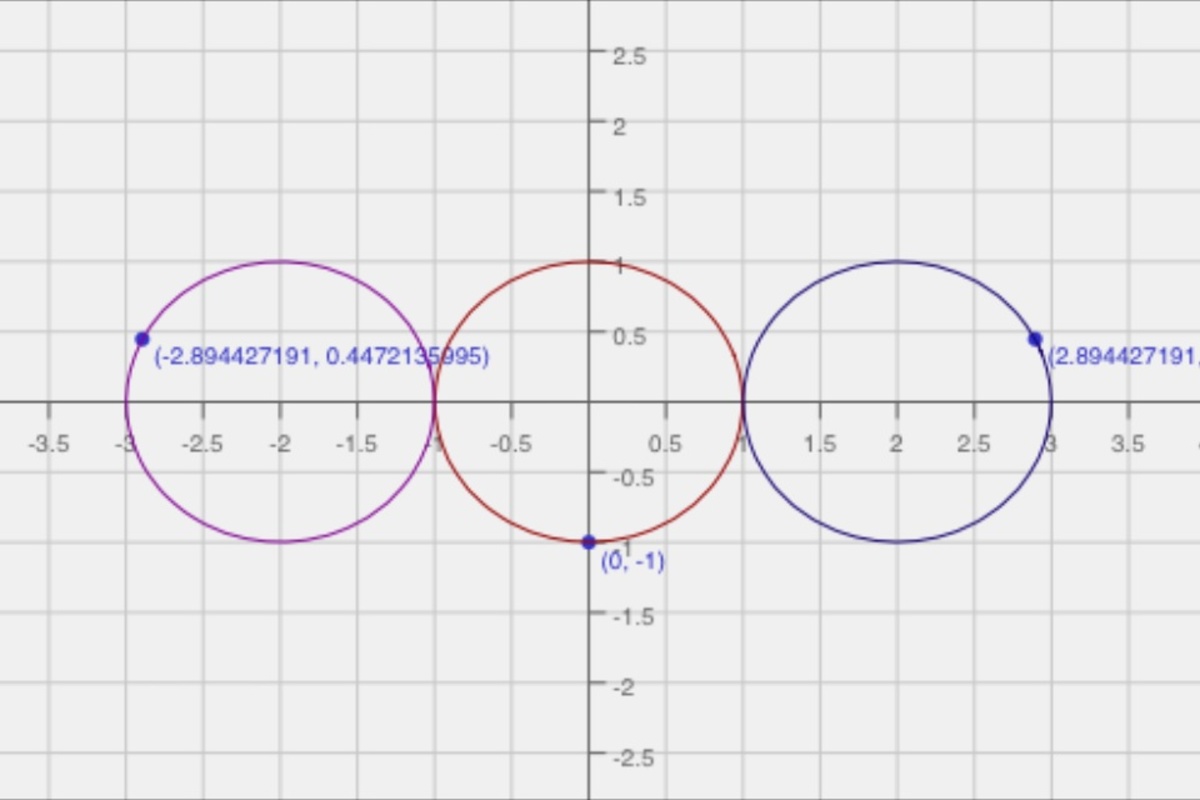
Consider the three unit circles above with the first and third ones touching the middle one and all their centers on the $x$ -axis. From the point $(0,-1)$ , locate the point on each of the other circles farthest from it. Connect these three points to form a triangle .

The most simplified ratio of the area of triangle to the sum of areas of the three circles can be expressed in this form

$\dfrac a{b\pi} ( c + \sqrt d) ,$

where $a,b,c$ and $d$ are positive integers with $a,b$ coprime and $d$ square-free. Find $a+b+c+d$ .

The answer is 27.

3 solutions

Ahmad Saad
Jul 20, 2016

Efren Medallo
Jul 19, 2016

We locate one of such point $P(x,\: y)$ by means of Pythagorean Theorem, and some light maxima-minima type of calculus.

Focusing on the rightmost circle, the distance $d$ of any point in the upper half of the circle to $(0, -1)$ is determined by

$d^2 \: = \: x^2 \: + \: (1\: + \:y)^2$

where $y \: = \: \sqrt{1\: - \: (x\: - \: 2)^2 }$

simplifying, we get

$d^2 \: = \: (4x \: - \: 2\: + \:2\sqrt{1\:-\:(x-2)^2}$

getting the derivative of the L.H.S with respect to $x$ , we get

$(d^2)'\: = \:4\: -\: \frac{2(x\:-\:2)}{\sqrt{1\:-\:(x-2)^2}}$

setting this to zero, we simplify this and get

$5(x\:-\:2)^2 \: = \:4$

$x \: = \: 2 \: + \: \frac{2\sqrt{5}}{5}$

from which

$y \: = \: \frac{\sqrt{5}}{5}$

well, basically, we have already found half the base of the triangle, and the height (1+y). Thus, multiplying this two and we get the triangle's area! Voila, we get

$A_{\Delta}\: = \: \frac{4}{5}(3\: + \: \sqrt{5})$ .

We just divide this by $A_{O} \: = \: 3\pi$ and we get

$\large \frac {4}{15\pi} (3+ \sqrt{5})$

This gives us $\large \boxed {4\: + \: 15 \: +3 \: + \: 5 \: = \: 27}$ .

The height of the triangle is $1+\frac{1}{\sqrt{5}}$ , not $\frac{1}{\sqrt{5}}$

Michael Mendrin - 4 years, 11 months ago

Oops. I keep doing mistakes like this. Thanks for that!!! I will do the changes in my solution.

Efren Medallo - 4 years, 11 months ago

@Efren Medallo, please tell where am i wrong

Let the point farthest from (0, -1) to extreme left circle be $C(-2+cos\theta , sin\theta)$ by using parametric coordinates.

Then other point on the extreme right circle farthest from (0, -1) must be the reflection of point C in y-axis.

So, let this point be ${C}_{1}(2+cos\theta, sin\theta)$ again by parametric coordinates.

So, resulting triangle has base parallel to x-axis.

We want to maximize distance between (0, -1) and C.

Which is $4\cos { \theta } +\sin { \theta } +6$

To maximize , differentiate it and make equal to 0; we get $\tan { \theta } =\frac { 1 }{ 4 }$

So, area of triangle is

$\huge\ \frac { \frac { 1 }{ 2 } \times 4\times \left( 17+\sqrt { 17 } \right) }{ 3\pi }$

which is giving another answer.

pLease tell where i am wrong.

Priyanshu Mishra - 4 years, 7 months ago

Niranjan Khanderia
Sep 28, 2016

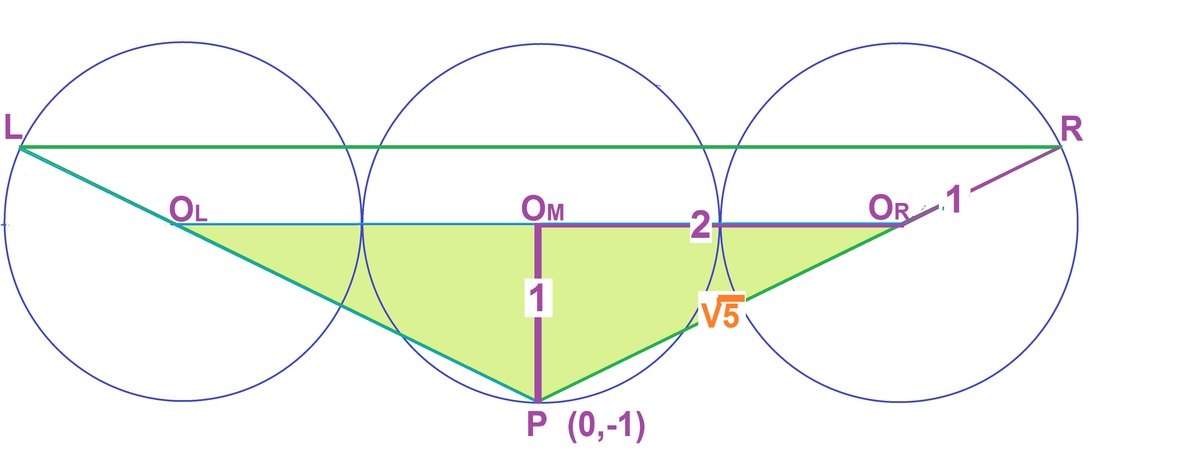
$Let\ the\ centers\ be\ O_L,\ O_M,\ O_R,\ and\ the\ triangle\ LRP,\ P(0, -1).\\ Area\ \Delta\ O_LO_RP=\frac 1 2 *O_LO_R*O_MP=\frac 1 2*4*1=\color{#3D99F6}{2}.\\ \text{In order that L, and R be farthest, they should be on point of tangentcy to respective circles. }\\ \text{So PR must pass through O\_R, and O\_RR the radius of right circle. Similarly for the left.}\\ \text{Because of symmetry, }LR || O_LO_R.\\ PO_R=\sqrt{(PO_M)^2+(O_MO_R)^2}=\sqrt{1+4}=\color{#3D99F6}{\sqrt5 ,\ and\ PR=1+\sqrt5}.\\ \therefore\ {Area\ LRP}=\left (\dfrac{PR}{PO_R}\right )^2*\{Area\ O_LO_RP\},\\ \ \ \ \ \ =\dfrac{6+2\sqrt5} 5*2=\color{#3D99F6}{\dfrac{4(3+\sqrt5)} 5}.\\ Desired \ ratio={\dfrac{4(3+\sqrt5)} 5}*\dfrac 1 {3\pi*1^2}.\\ \therefore\ a+b+c+d=4+15+3+5=\Large\ \ \ \color{#D61F06}{27}.$

The Farthest Point

The answer is 27.

3 solutions

0 pending reports