The field distorting sphere

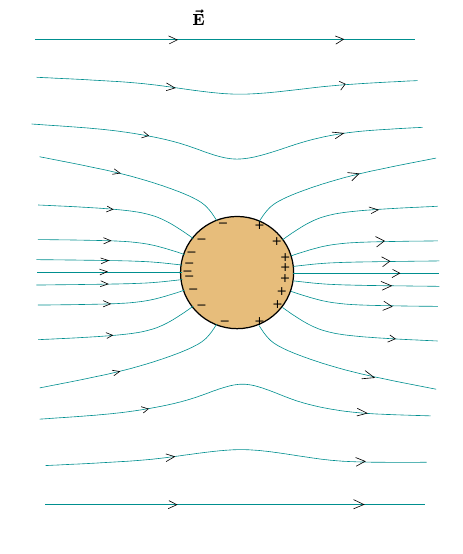
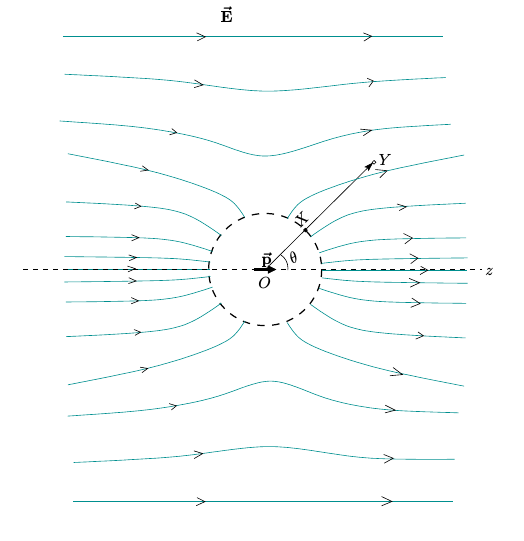
The standard solution will require us to solve the Laplace equation with suitable boundary conditions. That I'll leave for someone else to write down. I shall, on the other hand, look at a more elementary solution. Refer to the diagram shown in (a) below in the comments. Owing to the external field charges get induced on the sphere which bend the field lines. As the conducting sphere is an equipotential region, field lines must enter or leave it normally. The induced charges being equal and opposite form effectively a dipole oriented parallel to the (original) external field. As such, we can think of the resulting field pattern outside the sphere to be the superposition of the uniform external field and the field of a tiny dipole sitting at the center (whose magnitude we shall figure out shortly). Something similar to diagram shown in (b). Of course, this is not vaild for points inside the sphere. The dipole moment $p$ must be chosen so that the boundary conditions are exactly right. This means that on the (hypothetical) sphere of radius $R$ the dipole potential and external field potential should add up to zero. As the situation is symmetric around the $z$ axis, the potential does not depend on the azimuthal angle $\varphi$ .

The potential of a point dipole at a point $(r,\theta)$ is given by $V_\text{dip} = \dfrac{p\cos\theta}{4\pi\epsilon_0 r^2}$ While taking the reference for potential at the center O, the potential of the uniform field is $V_0 = -E_0z$ Consider the point $X$ on the sphere. We require the total potential to be zero. Considering that for this point $z=R\cos\theta$ , we get $0=V_\text{tot} = V_\text{dip}+V_0 = \dfrac{p\cos\theta}{4\pi\epsilon_0 R^2} - E_0 R\cos\theta$ so that we must take $p=4\pi \epsilon_0 E_0R^3$ . And with this choice of $p$ , we get the total potenital at $Y(r,\theta)$ as $V_\text{tot} = V_\text{dip}+V_0 = \dfrac{E_0R^3\cos\theta}{ r^2} - E_0 r\cos\theta$ i.e. to say that $\boxed{V_\text{tot}(r,\theta) =E_0\left( \dfrac{R^3}{ r^2} - r\right)\cos\theta \quad (r\ge R)}$ Hence $V(2R, \pi/3) = -\dfrac{7E_0R}{8}$ while $V(3R, -\pi/3) = -\dfrac{13E_0R}{9}$ . Hence their ratio is $\dfrac{63}{104}$ so that $a=63$ and $b=104$ . As a result, we get our final answer as $\boxed{167}$ .