Christmas Math Problem Set 2017 - A Triangle in a Square Tree
An elf at Santa's workshop was outside chopping down a Christmas tree when suddenly, a gust of wind blew the hat off of his head and carried it up into the tree:
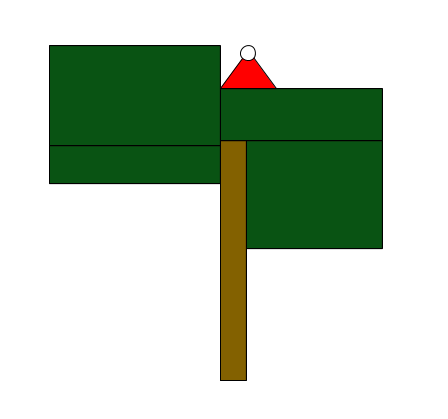
As can be seen in this picture, all of the different sectors of the tree are rectangles, and the height and width of some parts of the tree are equal in some areas. The elf also found a piece of paper crumpled in the snow that read the following:
Lumberjack's Notes
- The top left-most sector of the tree is a square.
- The shorter sides of the bottom-left most sector and the top right-most sector are equal. These two sectors are also equal in area.
- The width of the base of the tree is 6 units.
- The area of the top left-most sector is 67 units more than the area of the bottom right-most sector.
The elf needs to get a ladder to retrieve the hat, but he also needs to make sure that the ladder is long enough before he goes to get it. In order to do this, the elf needs to find the length of the right side of the bottom right-most sector, but he is having difficulty figuring it out. If we can assume that all of the side lengths of the rectangular sectors of the tree are positive integers, where is an integer under all circumstance, help the elf find the value of this side length.
This problem is part of: Christmas Math Problem Set 2017
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can start by setting all of the sides equal to variables. We take the picture of the tree and label it like this:
From the note, we can then set up some equations. We know that the area of the top right-most sector is a square, so we can express the area as b 2 . We know that area of the bottom left-most sector is equal to that of the top right-most sector, and the shorter sides of these two sectors are equal. We can set up this equation as: y ( x + 6 ) = b y , therefore ( x + 6 ) = b . We also know that the area of the top left-most sector is 6 7 units more than that of the bottom right-most sector, therefore b 2 = a x + 6 7 . Since b = ( x + 6 ) , we can substitute this into b 2 = a x + 6 7 , and get ( x + 6 ) 2 = a x + 6 7 . Expanding and bringing all of the terms to the left side of the equation: x 2 + ( 1 2 − a ) x − 3 1 = 0 . We know that x has a positive integer solution. If we wanted to solve this equation, we could realize that 3 1 is a prime number, and the only factorable forms of this equation, that would yield at least one integer solution to x are ( x − 1 ) ( x + 3 1 ) = 0 and ( x + 1 ) ( x − 3 1 ) = 0 . This means that in order for a to be an integer, 1 2 − a has to be 3 0 or − 3 0 , and since a must be a positive integer, 1 2 − a = − 3 0 , therefore a = 4 2 .