The flabbergasted engineer should do something quickly...
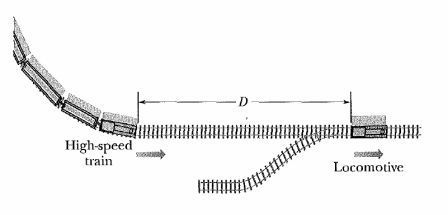 When a high-speed passenger train traveling at
rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance
ahead. The locomotive is moving at
. The engineer of the high-speed train immediately applies the brakes. What must be the magnitude of the resulting constant deceleration (in
) if a collision is to be just avoided?
When a high-speed passenger train traveling at
rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance
ahead. The locomotive is moving at
. The engineer of the high-speed train immediately applies the brakes. What must be the magnitude of the resulting constant deceleration (in
) if a collision is to be just avoided?
Liked it? try some more
The answer is 0.994.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Initial relative speed (u) = 161 - 29 = 132 kmph
Distance to be covered (s) = 676 m (limiting case for just avoiding the collision)
Final relative speed (v) = 0 kmph
From equation of motion,
v 2 − u 2 = 2 a s
Converting into appropriate units and solving,
a = − 0 . 9 9 4