The flight of the housefly
A housefly is sitting between the plates of a parallel-plate capacitor. The plates of the capacitor are disks of radius separated by a distance . The distance between the fly and the positive plate of the capacitor is with ( note that the fly is very close to the center of the capacitor). The housefly decides to exit the capacitor by flying along an equipotential line. What is the maximum distance in meters from the center of the capacitor the housefly reaches along the equipotential line?
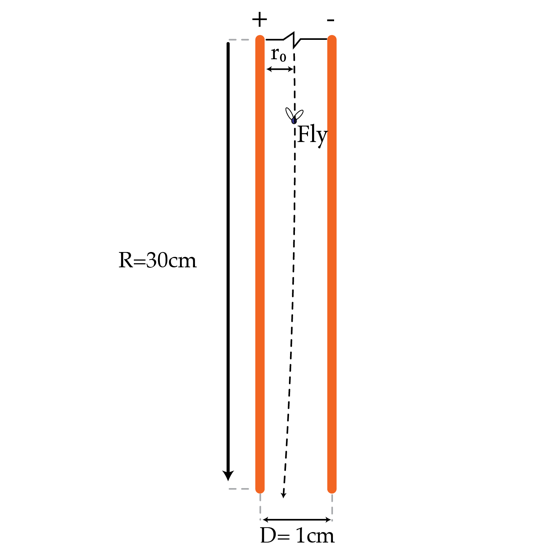
The answer is 21.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When the house fly is in the capacitor, because the field is uniform and it is obvious that the potential in the middle of the capacitor is zero, the potential of the fly is : V = E . 2 d ϵ = π R 2 ε Q . 2 d ϵ
since ϵ is very small, the potential is very small too. This potential can be obtained again when the fly is very far from the capacitor (the potential at that point is nearly zero). Hence, the capacitor cab be treated as a dipole with dipole momentum p = Q . d
The potential cause by a dipole is :
V = 4 π ε r 2 p sin α = 4 π ε r m a x 2 p
The ultimate equation is :
π R 2 ε Q . 2 d ϵ = 4 π ε r m a x 2 p t h e n r m a x = 2 ϵ R = 2 1 . 2 m