The Floo Network

Computer Science Level 1

Harry is going to be late to his class, so he needs to move as quickly as possible.

Here is a map of his institution, where the edges represent roads he could walk through, and the nodes of the same color are those between which he could teleport using the Floo Network:

What is the least number of roads he would need to walk through to get to the classroom?

Clarification: Teleportations happen instantaneously and thus are not included in the count.

Inspired by Christopher Boo

2 3 4 5

4 solutions

Jonathan Quarrie
May 22, 2017

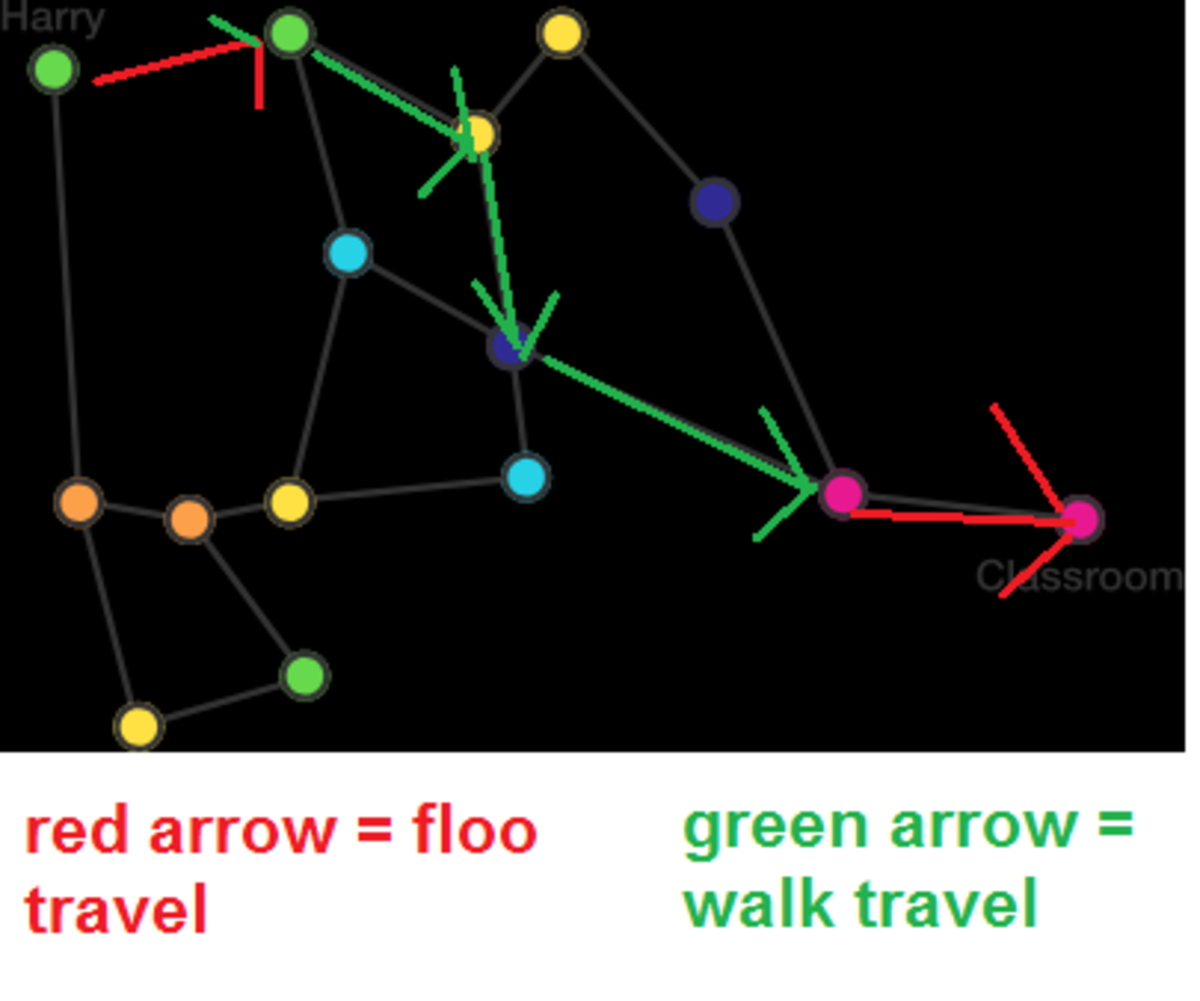
Paths traversed = $\large\boxed{3}$

There are other 3-path routes, but this was the easiest for me to animate.

In addition, @Kradak Thomas inspired the following image, which shows the network reduced down to just the connections that each colour makes (as all nodes of the same colour are equivalent). I encourage giving his solution an upvote too.

This proves that there aren't any 2-path solutions.

Moderator note:

In order to be complete a solution needs to show not only is a 3-path route possible, but a 2-path route is impossible. (There's a reduced version of the map in the comments which essentially accomplishes this.)

For those of us with red-green blindness, the green and yellow nodes, and the blue and purple nodes, are a bit hard to distinguish. One way to fix it would be to add a single letter label for each node where 'g' = green, 'y' = yellow etc.

Thomas Raffill - 4 years ago

That's an interesting point.

I could change my solution, but then that wouldn't help the people with red-green blindness that are still able to answer this problem.

The image on the problem needs to be changed in order to help those people. However, as I didn't write this problem, I can't change the image on it. Sorry.

Jonathan Quarrie - 4 years ago

This is a very cool animation. Thank you!

Agnishom Chattopadhyay - 4 years ago

Thanks! Thank you for the problem.

Jonathan Quarrie - 4 years ago

Can you find out an efficient way to solve this problem for larger road networks like this?

Agnishom Chattopadhyay - 4 years ago

Good question. I hadn't really thought about a generalised approach/method before you asked.

I imagine that Kradak Thomas's solution would lend itself well to a method of simplifying larger networks, by reducing the preconceived structure down to simple connections.

However, this wouldn't work with a problem such as your inspiration, where teleportations had limited uses.

Jonathan Quarrie - 4 years ago

Alternatively, you can also add 0-weight edges between all same-color nodes. Then run a Dijkstra's algorithm to find the shortest path.

Christopher Boo - 4 years ago

How do we know Harry won't transport from the blue node to the other blue node?

Mark Geha - 4 years ago

He can if he likes, that would still make it a 3-path route.

Jonathan Quarrie - 4 years ago

I thought you could only travel on the black lines...

Arliss Wolf - 3 years, 10 months ago

Abidur Rahman
May 18, 2017

steps = 0

Teleportation does not add to the step count, so first teleport to any of the green nodes. Move to the nearest yellow node. This adds 1 to the step count i.e. steps = steps + 1

Teleport to the yellow node on the top right corner. Again this does not add to the step count. Now take two steps forward to reach the pink node i.e. steps = steps + 2

You can now teleport to the final pink node. Therefore the total number of steps is 0 + 1 + 2 = 3.

How do show that it is not possible to do it in less that 3 steps?

Christopher Boo - 4 years ago

Doing it in less than 3 steps means that you would have to change colours less than 3 times. You start on green and want to go to pink, so that's 1 colour step. There is no green node around the pink nodes, instead there are blue nodes,so that's another step/colour swap. Finally, there is no green nodes around the blue nodes, so that's another step/colour swap. That means that you would have to do at least 3 steps or in other words 3 colour swaps.

Abidur Rahman - 4 years ago

Kradak Thomas
May 23, 2017

All color nodes are the same due to instant transport. You can redraw the graph to account for this. Edges that connect color nodes show the solution.

Green connects to orange, yellow and light blue by one step. Orange only points to Green and yellow. Yellow connects to light blue and blue. Light blue connects to blue. Blue connects to magenta (classroom)

Though I can't draw this here, you can check to see that two solutions exist: g-y-b-m and g-lb-b-m.

This is an interesting idea. Can we use this strategy to solve this problem efficiently for larger networks?

Agnishom Chattopadhyay - 4 years ago

Caillen Tu
Jun 4, 2020

It is 3 because ...

The Floo Network

4 solutions

Moderator note:

0 pending reports