The force it applies.
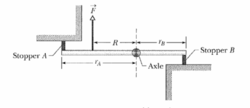 Figure above is an overhead view of a rigid rod that turns
about a vertical axle until the identical rubber stoppers A and B
are forced against rigid walls at distances
and
from the axle. Initially the stoppers touch the walls without being
compressed. Then force
of magnitude
is applied perpendicular
to the rod at a distance
from the axle.
Find the magnitude of the force compressing Stopper A.
Figure above is an overhead view of a rigid rod that turns
about a vertical axle until the identical rubber stoppers A and B
are forced against rigid walls at distances
and
from the axle. Initially the stoppers touch the walls without being
compressed. Then force
of magnitude
is applied perpendicular
to the rod at a distance
from the axle.
Find the magnitude of the force compressing Stopper A.
Liked it? try some more
The answer is 119.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This problem should accept the answer of 118!
Here's the solution:
You have the torque equation:
F R = f a r a + f b r b
Let's say the rod moves through an angle d θ when the stoppers are compressed. Now let's assume the force from the stoppers is proportional to the distance that they are compressed.
That gives us: k r a d θ = f a and k r b d θ = f b
But since they are identical, they will have the same constant of proportionality ( k ) so you get the relationship:
r a f a = r b f b
Now you have two equations and two unknowns so you can solve for f a and f b like any other system of equations.
I won't show the algebra, but you will find that f a , to the nearest integer, is 118N.
If you round it to the correct number of significant digits, then you get 120N