The Frozen Lake
 A group of scientists is given the job to determine the thickness of ice in a frozen lake. Ice being a good insulator of heat, one can find liquid water below a certain depth from the surface. However, the scientists don't have a meter-tape that is long enough to reach the water level, neither can they use a submarine to pierce through the ice. All they are given is a laser-pointer and a highly accurate timer.
A group of scientists is given the job to determine the thickness of ice in a frozen lake. Ice being a good insulator of heat, one can find liquid water below a certain depth from the surface. However, the scientists don't have a meter-tape that is long enough to reach the water level, neither can they use a submarine to pierce through the ice. All they are given is a laser-pointer and a highly accurate timer.
Let's assume the ice in the lake is a transparent material, whose refractive index varies as a linear function of the depth. It is known that the refractive index at the surface is μ 1 = 1 . 5 , and that at the lowest ice layer is μ 2 = 3 .

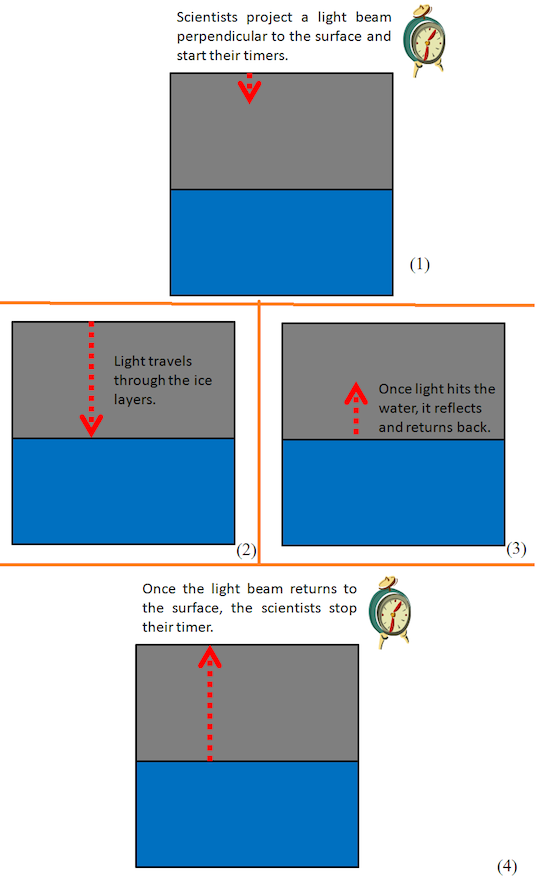
The scientists project a laser beam perpendicular to the surface and start their timer. The beam travels through the ice, hits the water, and reflects back. The scientists turn their timer off as soon as they see the laser beam return. It turns out that the time recorded on the timer is T = 5 × 1 0 − 6 seconds . What is the thickness h of the ice in meters, rounded to the nearest integer?
Details and assumptions
- Note that this experiment cannot be done in real life, as ice is an opaque material and water isn't a good reflector of light.
- The speed of light in vaccum is c = 2 9 9 , 7 9 2 , 4 5 8 m/s .
- If h in meters is of the form k + 0 . 5 for some integer k , enter k + 1 as your answer.
- The refractive index of ice varies as a linear function of depth simply means the refractive index at depth d below the surface is given by μ d = f ( d ) , where f is a linear polynomial.
- Reflex errors of the scientists are to be neglected.
Image credit: Ariel Bravy
The answer is 333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
Nice solution! My approach is a bit different though. It follows directly from Fermat's principle that the time taken for the light beam to reach the water ( = 2 T ) equals c 1 0 ∫ h μ x d x .
sir can you plz explian fermat's rule
In short form, it states that,
If a light beam has to travel from a point
A
to a point
B
, then it will do so such that it takes the least amount of time.
Another possibility seems to be treat the change in refractive index (and hence velocity) with depth similar to the constant of acceleration (g or a) in the basic equations of motion , v = u + a t (v being c/3) and u being (c/1.5) and t being the total time (or rather half of the total return time). Then we go on to find the total height as h=s(total distance) = u t + 1/2 a t^2
That is, indirectly, the same process that is shown above. It is just another way to think about that process. You have suggested to apply equations of motion, I have done just that.
The only flaw in your suggestion seems to be that, you have assumed the acceleration to be constant , where in fact, it is not constant.
Since refractive index is linearly varying so we can find out mid point ((1.5+3)/2)and assume to be constant over height "h". Since we are observing the ray after 2T time where T denotes total time required before 2nd reflection rest is simple distance-speed calculation
best answer till now
the thinking was to easy to think... thats why... we could not... -_- :(
T
=
5
.
1
0
−
6
s
t
1
+
t
2
=
5
.
1
0
−
6
h
/
v
1
+
h
/
v
2
=
5
.
1
0
−
6
h
(
1
/
v
1
+
1
/
v
2
)
=
5
.
1
0
−
6
h
(
µ
1
/
c
+
µ
2
/
c
)
=
5
.
1
0
−
6
h
(
µ
1
+
µ
2
)
=
5
.
1
0
−
6
.
c
h
(
1
.
5
+
3
)
=
5
.
1
0
−
6
.
c
h
=
5
.
1
0
−
6
.
2
.
9
9
7
9
2
4
5
8
.
1
0
8
/
4
.
5
=
3
.
3
3
.
1
0
2
m
=
3
3
3
.
3
3
m
just read the 4th assumption + the 1st.
If the laser beam is projected perpendicularly how does it undergo refraction?
It does not refract......who said it does?
yeah sorry I misunderstood the problem
As R.I of ice is changing linearly , we can take its R.I as mean of 1.5 and 3 .i.e R.I=2.25. Therefore speed of light in ice is 1.33*10^2 m/s. Thus thickness is 332.5 .e.i=333 metres.
Since the Refractive Index is a linear function of distance,
If x represents a general depth inside the ice,
Then, by functional analysis, we have,
μ = 1 . 5 ( 1 + h x )
Now, By the real definition of Refractive Index, we know,
Speed of Light in a Medium ( v ) = μ c , where c is the speed of light in vacuum .
Therefore,
v = d t d x = 3 2 c h + x h
Rearranging,
( h + x ) d x = 3 2 c h d t
Integrating both sides,
∫ 0 h ( h + x ) d x = ∫ 0 t 3 2 c h d t
Note that t here, is only half the time. So, we will have to double it once we are finished.
2 3 h 2 = 3 2 c h t
⇒ t = 4 c 9 h
Doubling t ,
⇒ T = 2 t = 2 c 9 h = 5 × 1 0 − 6 sec (as given)
Simplifying, and using the values given,
h = 3 3 3 . 1 ≈ 3 3 3 m