The Game of The Spider and The Bug

Logic Level 3

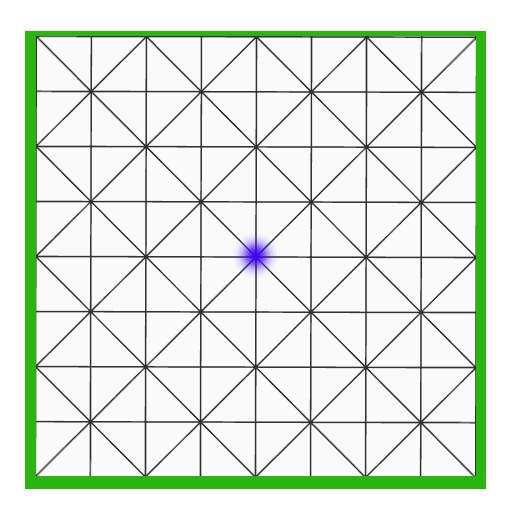The Spider's Web

The above diagram depicts a spider web, where the black lines are fibers of the web, and the intersections of the fibers are called junctions .

The spider caught a bug at the center of the web, which is marked by a blue dot, and plays the following game with the bug:

Step 1: At a junction, the bug picks a fiber (which passes through the point) to walk along.
Step 2: The spider chooses the direction along the fiber for the bug to walk along.
Step 3: The bug walks in that direction till he reaches the next junction.
Step 4: If the bug touches the boundary of the web (which is marked in $\color{#20A900}{\text{green}}$ ), the bug is allowed to escape. Otherwise, we return to step 1 and the bug picks another fiber.

Can the bug ever manage to escape?

Yes No

1 solution

Ojasee Duble
Mar 10, 2017

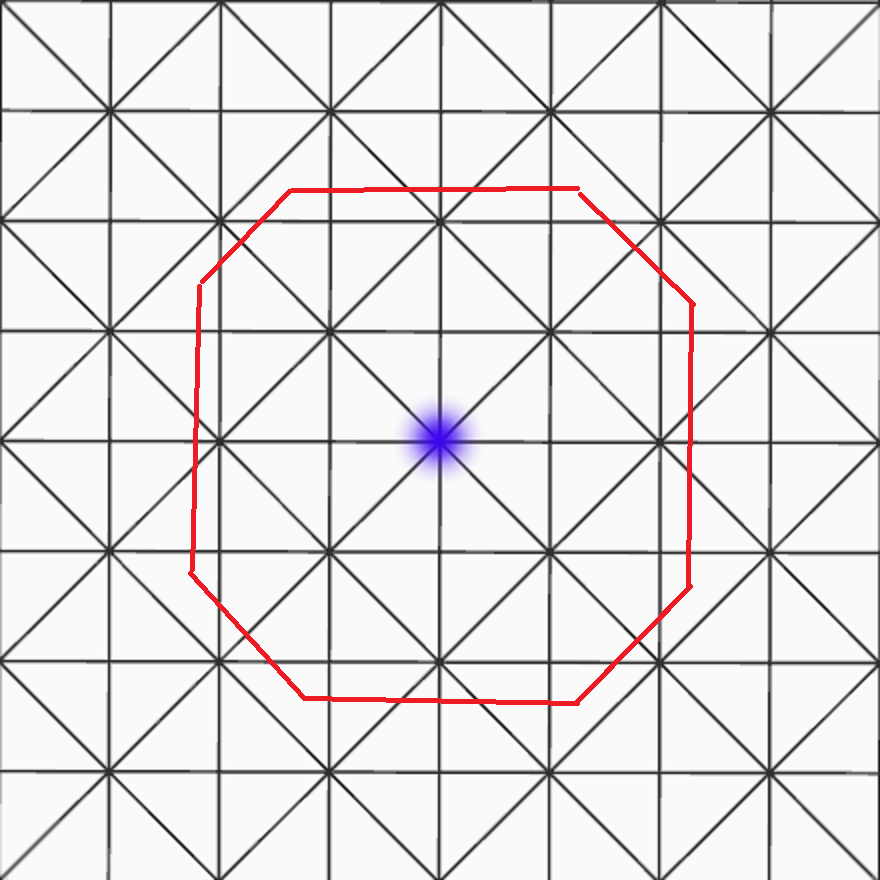
Every time the bug would be about to reach the boundary of the web, the spider may decide that bug may move backward preventing it to escape the web.

Hence, the bug can't escape the web.

I believe a more complete solution might be to consider this figure:

The bug can't escape from the red line since any time he is about to embark on a branch that intersects it, the spider can send him back the other way.

Note, Ojasee's solution doesn't quite work, since if you look at for example the node that is just SE of the upper left corner. If the bug decides to go NE, even if the spider reverses his direction, he still escapes!

Geoff Pilling - 4 years, 3 months ago

That is an interesting observation. The problem here being that not all the points are actually uniform.

What are the necessary conditions an arbitrary spider web should have so that the bug can always escape?

Agnishom Chattopadhyay - 4 years, 2 months ago

I believe that in order for the bug to be able to escape, then at every point where the spider can change his direction, there needs to be two paths that both lead him closer to the exit. In this case, for all the four way intersections that don't share either an x or y coordinate with the central blue point, this is not the case.

Geoff Pilling - 4 years, 2 months ago

The bug wins immediately when he touches the boundary. So, this is a non-solution

Agnishom Chattopadhyay - 4 years, 3 months ago

I didn't quite understand why it's a non-solution....

Ojasee Duble - 4 years, 3 months ago

(Ah, i see Geoff made this comment already)

Ojassee is saying something different than what Agnishom is interpreting. Let me translate.

Suppose that the bug were to reach the boundary in the next move. Then, all the spider needs to do is to select the opposite direction for the bug to walk in. Hence, the bug would never be able to reach the boundary.

Unfortunately, the second sentence is only true if "For each junction, there isn't a fiber that is directly connected to the boundary on both sides". This does not hold true, like if the spider was at the junction in the upper left corner, and chooses the north-east to south-west fiber.
Of course, we can try and make the argument that "the bug will not reach that junction", so on and so forth.

Calvin Lin Staff - 4 years, 2 months ago

The Game of The Spider and The Bug

1 solution

0 pending reports