The Gold Pentagon

The interior angle of a regular pentagon is $108°$ , and by symmetry $BG = BJ = JF$ . Since a straight line is $180°$ , $\angle BGJ = \angle BJG = 180° - 108° = 72°$ , and by vertical angles $\angle BJF = 108°$ . Since the angle sum of a triangle is $180°$ , $\angle GBJ = 36°$ , and since $\triangle BJF$ is an isosceles triangle, $\angle JBF = \angle JFB = \frac{180° - 108°}{2} = 36°$ .

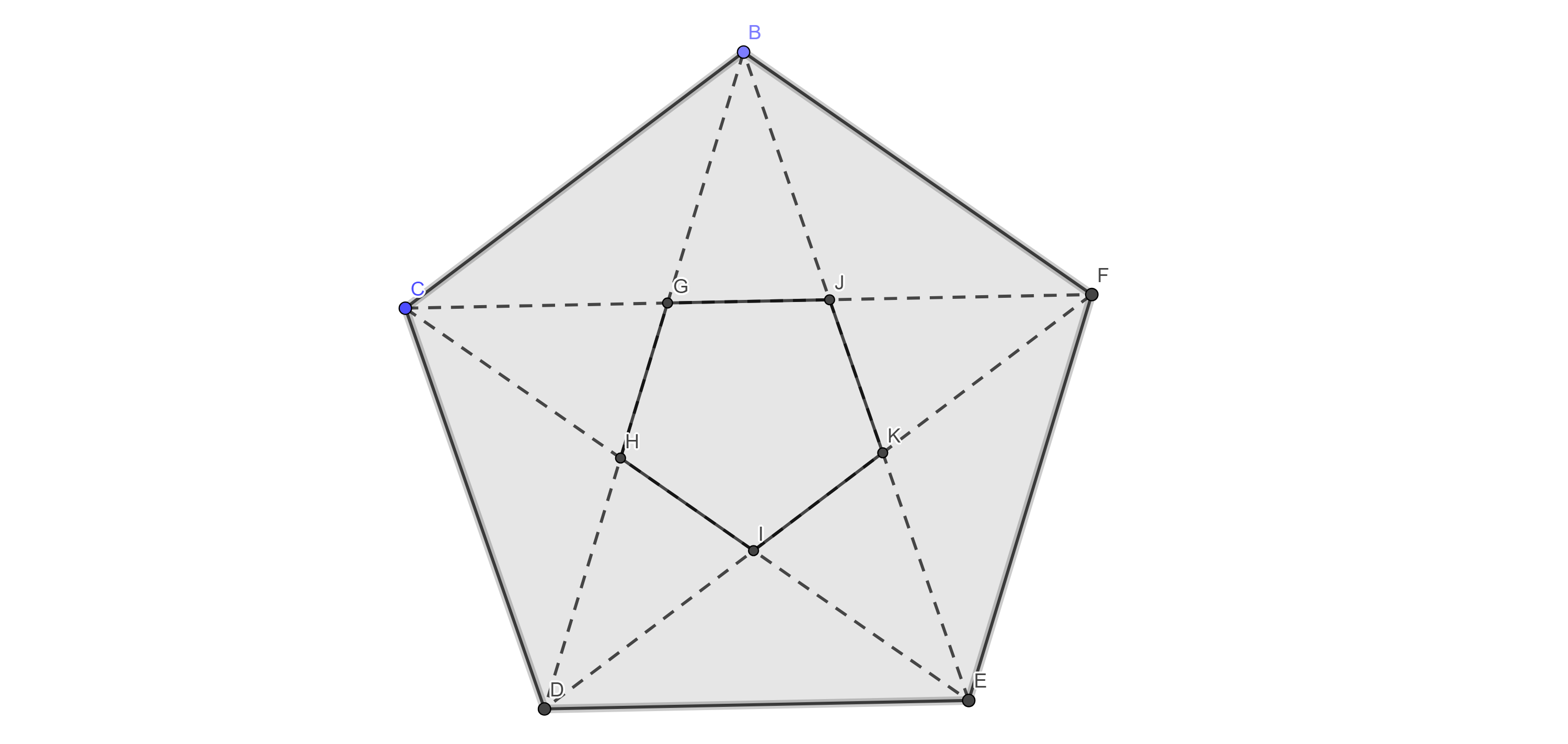
Let $x$ be the side of the small regular pentagon, and let $1$ be the side of the big regular pentagon, so that $GJ = x$ and $BF = 1$ . Since $\angle FBG = \angle FGB$ , $\triangle FBG$ is an isosceles triangle and $BF = GF = 1$ . That means $JF = GF - GJ = 1 - x$ , and $BG = BJ = JF = 1 - x$

Since $\triangle FGB \sim \triangle BGJ$ by AA similarity, $\frac{1}{1 - x} = \frac{1 - x}{x}$ , and this solves to $x = \frac{3 - \sqrt{5}}{2}$ for $x < 1$ . The ratio of the sides of the small pentagon to the big pentagon is $\frac{x}{1} = \frac{3 - \sqrt{5}}{2}$ , and the ratio of the areas is the square of this, which is $x^2 = (\frac{3 - \sqrt{5}}{2})^2 = \frac{7 - 3\sqrt{5}}{2} \approx \boxed{0.145898034}$ .

(Incidentally, this ratio is also $\frac{1}{\phi^4}$ , where $\phi = \frac{1 + \sqrt{5}}{2}$ , the golden ratio.)

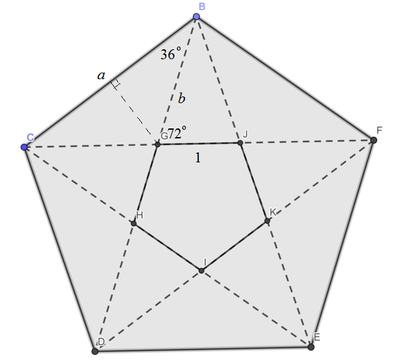
Let the side length of the small regular pentagon $GJ = 1$ , the side length of the big regular pentagon $BC = a$ , and the length \(BG=b). Since area of similar shape is directly proportional to the square of linear dimension, we have:

\(\begin{align} \frac AB & = \frac 1{a^2} & \small \color{blue} \text{Note that }a = 2b \cos 36^\circ \\ & = \frac 1{(2b\cos 36^\circ)^2} & \small \color{blue} \text{and }b = \frac {\frac 12}{\cos 72^\circ} \\ & = \frac {\cos^2 72^\circ}{\cos^2 36^\circ} \\ & = \left(\frac {2\cos^2 36^\circ - 1}{\cos 36^\circ}\right)^2 \\ & = \left(2\cos 36^\circ - \frac 1{\cos 36^\circ}\right)^2 & \small \color{blue} \text{also } \cos 36^\circ = \frac {1+\sqrt 5}4 \text{ (see note)} \\ & = \left(\frac {1+\sqrt 5}2 - \frac 4{1+\sqrt 5}\right)^2 \\ & = \left(\frac {\sqrt 5-1}{\sqrt 5+1}\right)^2 = \left(\frac {3-\sqrt 5}2 \right)^2 \\ & = \frac {7-3\sqrt 5}2 \approx \boxed{0.146} \end{align} \)

---

Note: Note that $\cos 36^\circ = \cos \frac \pi 5$ and

$\begin{aligned} \cos \frac \pi 5 + \cos \frac {3\pi}5 & = \frac 12 \\ \cos \frac \pi 5 - \cos \frac {2\pi}5 & = \frac 12 \\ \cos \frac \pi 5 - 2\cos^2 \frac \pi 5 + 1 & = \frac 12 \\ 4\cos^2 \frac \pi 5 - 2\cos \frac \pi 5 - 1 & = 0 \\ \implies \cos \frac \pi 5 & = \frac {1+\sqrt 5}4 \end{aligned}$