The Golden Area.
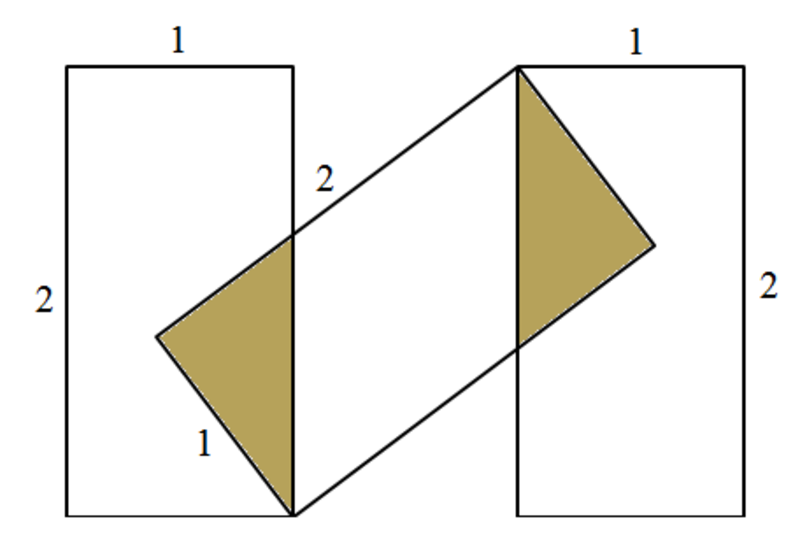
Three 2 × 1 rectangles are arranged as shown. What fraction of the figure is golden?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for sharing your solution.
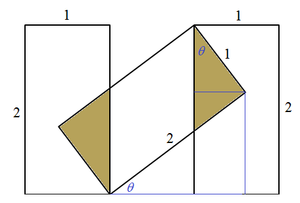
Due to symmetry, the two golden right triangle are congruent. Let the smallest vertex angle of the golden triangle be θ as shown. We note that:
cos θ + 2 sin θ 1 + t 2 1 − t 2 + 1 + t 2 4 t 3 t 2 − 4 t + 1 ( 3 t − 1 ) ( t − 1 ) ⟹ t = 2 = 2 = 0 = 0 = 3 1 Using half-angle tangent substitution and let t = tan 2 θ t = 1 is rejected because θ = 2 π
Note that the area of a golden triangle is 2 1 tan θ . Therefore, area of the golden region A g = tan θ = 1 − t 2 2 t = 4 3 . The area of the figure is A F = 6 − A g = 6 − 4 3 = 4 2 1 and A F A g = 4 3 × 2 1 4 = 7 1 .
Thank you Sir.
Label the diagram as follows and draw A D and D E :
Since ∠ B = ∠ E = 9 0 ° , B D = A E = 2 , and A D = A D , △ A E D ≅ △ D B A by the hypotenuse-leg congruence theorem.
Since A B = D E = 1 by congruent parts, ∠ D C E = ∠ A C B by vertical angles, and ∠ B = ∠ E = 9 0 ° , △ C E D ≅ △ C B A by the AAS congruence theorem.
Letting B C = C E = x , then A C = C D = x 2 + 1 by Pythagorean's Theorem, and A E = A C + C E = x 2 + 1 + x = 2 which solves to x = 4 3 .
Therefore the golden area is A G = 2 ⋅ 2 1 ⋅ 1 ⋅ 4 3 = 4 3 , the white area is A W = 3 ⋅ 1 ⋅ 2 − A G = 6 − 4 3 = 4 2 1 , and the fraction is A W A G = 4 2 1 4 3 = 7 1 .