Absolute Value System
∣ a − b ∣ ∣ b − c ∣ ∣ c − d ∣ = = = 2 3 4
Given that a , b , c , d are real numbers that satisfy the system of equations above, what is the sum of all distinct values of ∣ a − d ∣ ?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Very convincing solution.
Simplest! This is good.
Seriously a good solution explaining why the values were taken like this!
I just did +-2 + +-3 + +-5 + +-9 and ended up with zero. ahhhhhh....!
Same method. Nice and short solution
Solution is precise. Thought in a similar way.
Same solution but yours is much neater. Nice!
Took me a little while to get, but that's innovative.
Quite comprehensive
almost missed it because i put 0 on the first time ... its |a-d| not a-d o.o
a − d = ( a − b ) + ( b − c ) + ( c − d ) & a − b = ± 2 , b − c = ± 3 , c − d = ± 4 , & a − d = ( a − b ) + ( b − c ) + ( c − d ) S o ( a − d ) w i l l h a v e 8 v a l u e 4 p a i r ( o n e + v e & o n e − v e ) h a v i n g 4 n u m e r i c a l l y d i f f e r e n t v a l u e , A n s = ( 2 + 3 + 4 ) + ( − 2 + 3 + 4 ) + ( 2 − 3 + 4 ) + ( 2 + 3 − 4 ) = 1 8
Good solution! The key part of this question was to write a − d as ( a − b ) + ( b − c ) + ( c − d ) .
Log in to reply
I highly doubt that this was a KVPY problem since this is just too easy.
Log in to reply
Same here ! Such problems are a jackpot in such tests.
From ⎩ ⎪ ⎨ ⎪ ⎧ ∣ a − b ∣ = 2 ∣ b − c ∣ = 3 ∣ c − d ∣ = 4 ⇒ b = a ± 2 ⇒ c = b ± 3 ⇒ d = c ± 4
Therefore, the possible values of d and ∣ a − d ∣ for each a are as follows:
⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ b = a − 2 ⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ c = a − 5 ⇒ { d = a − 9 ⇒ ∣ a − d ∣ = 9 d = a − 1 ⇒ ∣ a − d ∣ = 1 c = a + 1 ⇒ { d = a − 3 ⇒ ∣ a − d ∣ = 3 d = a + 5 ⇒ ∣ a − d ∣ = 5 b = a + 2 ⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ c = a − 1 ⇒ { d = a − 5 ⇒ ∣ a − d ∣ = 5 d = a + 3 ⇒ ∣ a − d ∣ = 3 c = a + 5 ⇒ { d = a + 1 ⇒ ∣ a − d ∣ = 1 d = a + 9 ⇒ ∣ a − d ∣ = 9
Therefore, the sum of possible values of ∣ a − d ∣ is 1 + 3 + 5 + 9 = 1 8
I thought of a similarly way
same approach i did
Hi, Sir can you please tell us how expressions involving ( a - constant ) becomes the new expressions , a - d = constant .. i.e. the last column such as a - 9 => a - d = 9
Log in to reply
d = a − n ⟹ ∣ a − d ∣ = ∣ a − a + n ∣ = ∣ n ∣ = n . I have changed the solution for easy understanding.
(a-b)=2 or (a-b)=-2 (b-c)=3 or (b-c)=-3 (c-d)=4 or (c-d)=-4 (a-d)=(a-b)+(b-c)+(c-d) = 2+3+4 (a-d) = 9 Mod on both side |(a-d)|= 9 .........(x) (a-b)=-2 (b-c)=-3 (c-d)=-4 (a-d)=(a-b)+(b-c)+(c-d) = (-2)+(-3)+(-4) (a-d) = -9 Mod on both sides |(a-d)| =| -9| |(a-d)|= 9 .........(Y) Adding (x) and (Y) Sum of distinct values of |(a-d)| would be= 9+9=18
Same method as me. The neatness of the formatting of this solution is amazing.
I like this solution! A much more graphical method than the others providing a unique way to obtain the solution! Would possibly be quicker than the other methods maybe?
did exactly the same way.
exactly the same solution. this is the real meaning of absolute value------the distance between numbers
Best solution :)
hmmm.....There are multiple answers to this since the absolute values are taken. The difference are known to be 2 3 4, so you can add all of them to get 9. But you can also add/subtract them in ways to get answers of 5, 3, and 1.
Yeah i think 9 should also be reasonable but it is not counted
" What is the sum of all possible values of"
Can you explain with a little more detail? Actual equations, maybe?
Obviously, 'a' can be viewed as a reference point, and it doesn't change the value of |a-d|. So set a =0. ∣ d ∣ = ∣ d − c + c − b + b ∣ = ∣ ± 4 ± 3 ± 2 ∣ ∈ { 1 , 3 , 5 , 9 }
∣ a − d ∣ = ± 2 + ± 3 + ± 4
by drawing the tree, it's easily found that the possible values of |a-d| are: 1,3,5, 9.
thus, the sum is 18
I did it in a very childish way by supposing a to be 4 and then brute forcing to calculate b and c which gave me 4 distinct values for c. When I reached d I had 8 values out of which 6 were distinct. When I got absolute values for the difference between 4 and those values got 6 values out of which 4 were distinct namely 1 3 5 and 9. Thus making the sum as 18.
There are basically two possibilities for the value of each (a-b), (b-c) and (c-d) as 2 or -2, 3 or -3 and 4 or -4 respectively, hence we have 8 different possible combinations as under;
- a-b=+2, b-c=+3, c-d=+4 -> a-d=+9
- a-b=+2, b-c=+3, c-d=-4 -> a-d=+1
- a-b=+2, b-c=-3, c-d=+4 -> a-d=+3
- a-b=+2, b-c=-3, c-d=-4 -> a-d=-5
- a-b=-2, b-c=+3, c-d=+4 -> a-d=+5
- a-b=-2, b-c=+3, c-d=-4 -> a-d=-3
- a-b=-2, b-c=-3, c-d=+4 -> a-d=-1
- a-b=-2, b-c=-3, c-d=-4 -> a-d=-9
From 1 and 8 we get |a-d|=9, From 2 and 7 we get |a-d|=1, From 3 and 6 we get |a-d|=3, and From 4 and 5 we get |a-d|=5.
Hence 9+1+3+5=18 :)
It can be solved by using the number line. First place a and b, and then check for possible locations of c, and the corresponding location of d. c cannot be between a and b. c can either be before a or after b or vice versa. Which give only four possible locations of d. Correspondingly, the distance between a and d has four possible values: 9,3,1,5. So, the sum comes out to be 18.
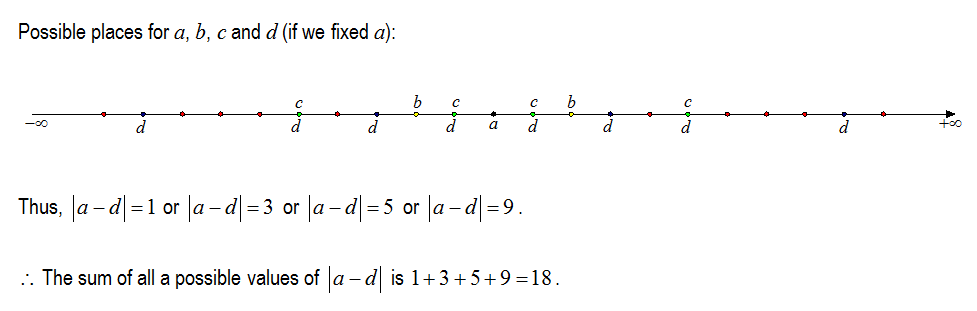
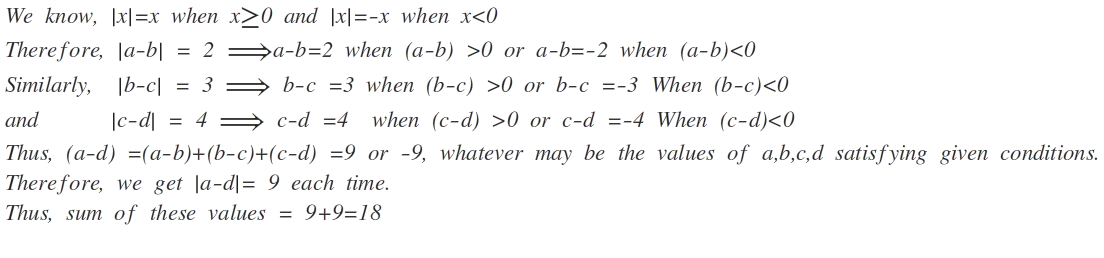
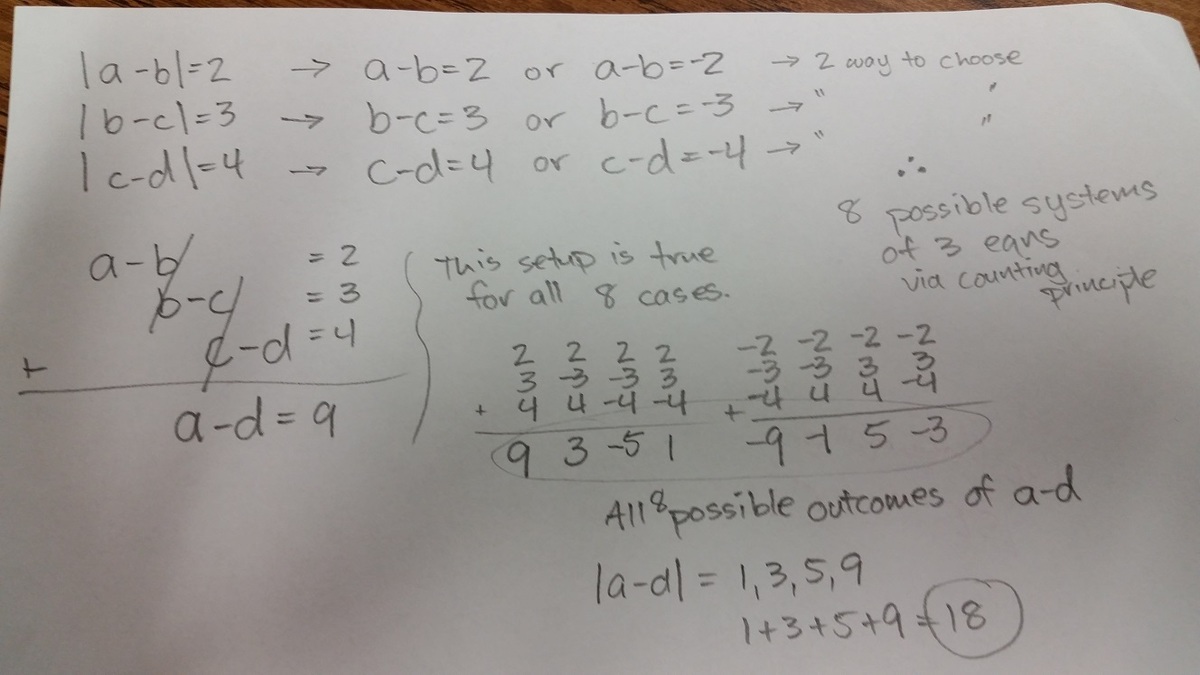
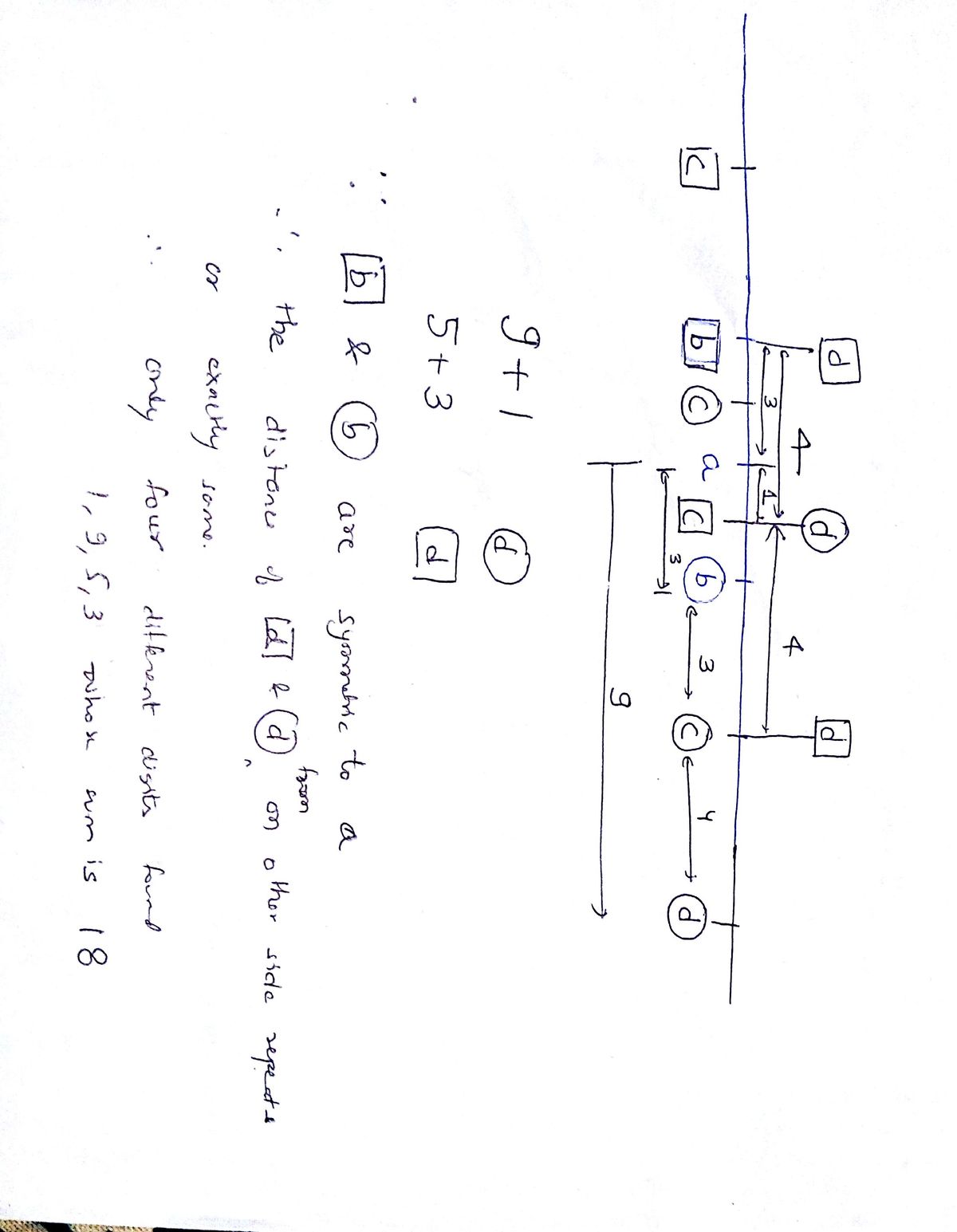

a − d = ( a − b ) + ( b − c ) + ( c − d ) = ± 2 + ± 3 + ± 4 ∈ { − 9 , − 5 , − 3 , − 1 , 1 , 3 , 5 , 9 } So ∣ a − d ∣ ∈ { 1 , 3 , 5 , 9 } , and 1 + 3 + 5 + 9 = 1 8 .