The Greatest Pyramid

Geometry Level 4

Pharaoh Pi-Ramides wishes to construct a limestone square pyramid to honour Thoth, the god of knowledge, with the least exposed surface area (all faces except for the base) to a given volume of bricks. He, along with the pyramid's architects, would like to know its sides' inclination relative to the base.

What, then, is the inclination of the faces, in degrees, relative to the base?

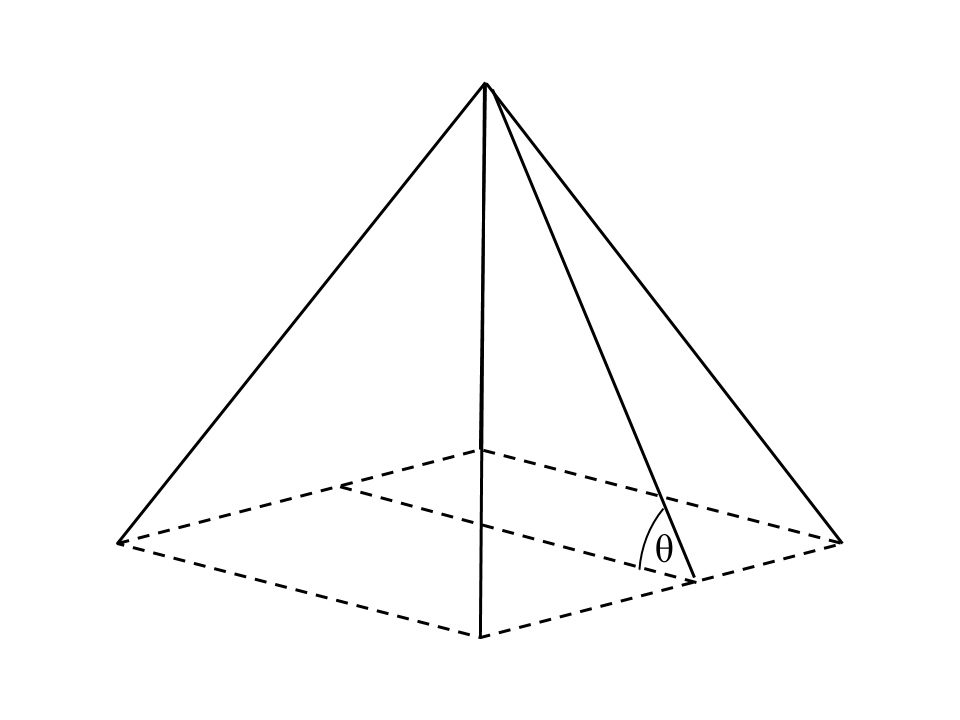
Assumptions:

  • The pyramid is a perfect square pyramid.
  • The pyramid is situated on a flat plane.
  • The base is perfectly level relative to the ground.

Note: This problem only requires knowledge of basic geometry and trigonometry. No calculus necessary!


The answer is 54.7356.

Andrei Li by Andrei Li , 16, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Michael Mendrin
Aug 2, 2018

Given a volume, a regular octahedron has the least surface area among irregular octahedrons. If the edge of the regular octahedron is 1 1 , then the diagonal is 2 \sqrt{2} , so that if it's cut in half to create a pyramid of a square base of side 1 1 , the angle of inclination is A r c T a n ( 2 ) = 54.7356 ArcTan(\sqrt{2})=54.7356 degrees.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

Is there another way to prove that ? I am a little bit confused, because when calculating the volume (V) and the lateral surface (S) of the pyramid with 54.7° and a square length (base) of 1, I get (if I did not make a mistake...) V=0.24 and S=0.43x4=1.732 (sqrt(3). The ratio S/V is about 7.5. When doing it with 60°, I get V=0.289 (sqrt(3)/6) ans S=2, S/V=6.928. I would say that with 60%, we have a least surface compared to volume. Where am I wrong ? Thanks.

Gerard Boileau - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...