The Greatest Sin

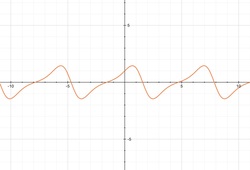
Well, this is quite an easy problem (compared to the rest of the problems in this set). It is set as a Calculus problem, so I'll simply use the first derivative test and the graph provided to find maxima of $f(x)$ .

$f(x)=e^{\sin(x)}\cos(x)\implies f'(x)=e^{sinx}\left(\cos^2 x-\sin x\right)$

Critical points of $f(x)$ (points of extremum, if any) are given by $f'(x)=0$ . Setting that, we have,

$\cos^2 x=\sin x\implies 1-\sin^2 x=\sin x\implies \sin^2 x+\sin x-1=0\\ \implies \sin x=\frac{-1\pm\sqrt{5}}{2}\implies \sin x=\frac{\sqrt{5}-1}{2}$

The other solution is rejected since it is $\lt (-1)$ and we are dealing explicitly with reals for this case. Now, comes the reasoning part. From the given graph, it is clear that maxima occurs in 1st quadrant in the principal range $[0,2\pi]$ and the value we obtained is also the sine of a first quadrant $x$ . So, it is our point of maximum. Hence, for positive solution of $\sin x$ , the value of $\cos x$ is also positive (note that we are talking about the point of maxima $x=x_{max}$ here). So, we have,

$\sin(x_{max})=\frac{\sqrt{5}-1}{2}\implies \cos(x_{max})=\sqrt{1-\sin^2 x}=\left(\frac{\sqrt{5}-1}{2}\right)^{1/2}$

Using these values, we have,

$max(f)=\left(\frac{\sqrt{5}-1}{2}\right)^{1/2}\cdot e^{\frac{\sqrt{5}-1}{2}}$

Comparing values with given form, we have $c=5,b=1,a=2$ .

Hence, we have the sum $=5+1+2=\boxed{8}$

---

$\textbf{Notes:}$

• $x_{max}$ denotes the point of maxima in $[0,2\pi]$ , in case you didn't bother to read every minute detail.

• We can also use the higher derivative test without relying on the graph.

lol, it's $\phi-1$ , I tried to hide it by doing $\left(\dfrac{\sqrt{c}-b}{a}\right)^{\frac{1}{a}}$ instead of $\sqrt{\dfrac{\sqrt{c}-b}{a}}$ . But idk how "unobvious" it is.

Here we take the derivative and set it equal to 0. differentiating

$0=\frac{d}{dx}~(e^{\sin(x)}\cos(x))$

Product rule $\Longrightarrow 0=\cos(x)~\frac{d}{dx}~e^{sin(x)}-\sin(x)e^{\sin(x)}$

Focusing on the derivative of $e^{\sin(x)}$ . And using the chain rule $(f(g(x)))'=f'(g(x))\cdot g'(x)$ . Setting $f(x)=e^x$ and $g(x)=\sin(x)$

$e^{\sin(x)}\cdot \cos(x)$

Putting this back into our old equation gives

$0=e^{\sin(x)}(\cos^2(x)-\sin(x))$

Since $e^{\sin(x)}$ has no roots, $\cos^2(x)-\sin(x)=0$

Doing some arithmetic and using the ever useful identity $\cos^2(x)=1-\sin^2(x)$

$(1-sin^2(x))-\sin(x)=0$

$\sin^2(x)+\sin(x)-1=0$

Quadratic eq

$\sin(x)=\dfrac{-1\pm\sqrt{5}}{2}$

Observe $f(x)$ is increasing as x increases (to a certain point, which is of course the maximum). Thus we ignore the - case. So

$\boxed{\sin(x)=\dfrac{-1+\sqrt{5}}{2}}$

Using the once again ever useful $\cos^2(x)=1-\sin^2(x)$

$\boxed{\cos(x)=\left(\dfrac{\sqrt5-1}{2}\right)^{\frac{1}{2}}}$

Thus the max value of our expression is

$\cos(x)e^{\sin(x)}=\left(\dfrac{\sqrt5-1}{2}\right)^{\frac{1}{2}}e^{\dfrac{\sqrt{5}-1}{2}}$

Thus $c=5$ and $a=2$ and $b=1$

So $\boxed{a+b+c=8}$