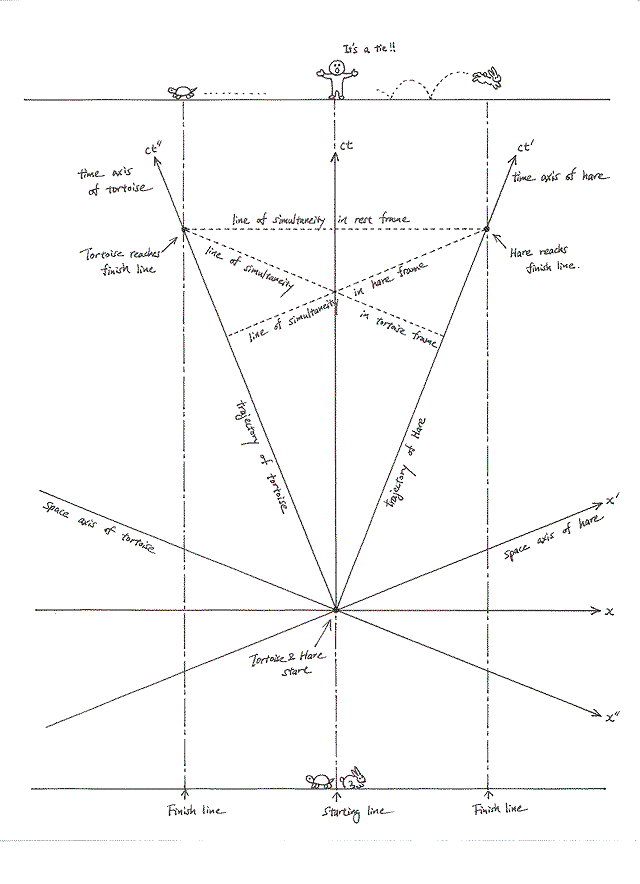
The Hare and the Tortoise Round 2
The hare and the tortoise decide to have another race. But instead of running in the same direction toward the finish line, they decide to run in opposite directions toward finish lines located at equal distances from the starting line as shown in the figure.
The race takes place and the referee sees both animals finish at the same time in the frame at rest with respect to the ground. Assuming that the two animals move at a constant velocity from start to finish, what is the result of the race as seen from the frames of the two moving animals?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you follow the line of simultaneity of the hare, the space-time point of the hare crossing the finish line is simultaneous with a space-time point on the tortoise's trajectory which is only about two thirds of the way to its finish line. So in the hare's frame of reference, it won the race. The exact same argument applies to the tortoise's frame of reference so it too thinks it won the race.