The Height is There
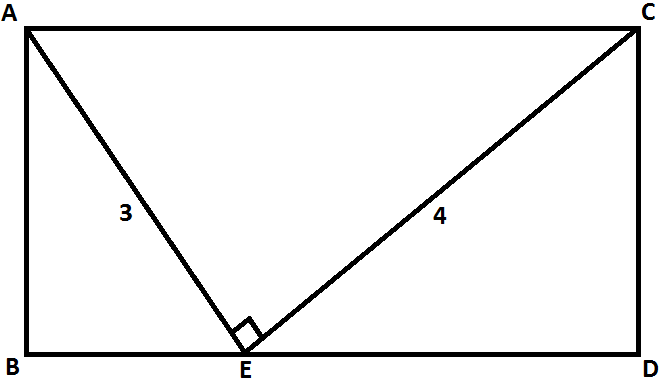
Assuming triangle is a right-angle triangle, , and , find the area of rectangle .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Because triangle A E C is right-angle, we can solve for the hypotenuse via the Pythagorean Theorem.
3 2 + 4 2 = c 2
2 5 = c 2
5 = c
Now, we need to find the length of line C D .
We observe that the area of rectangle A B D C = ( A C ) ( C D ) .
We established that A C = c = 5 , and therefore
2 ( 5 ) ( C D ) = 6
because C D can be considered a height if A C is the base.
By isolating the variable, we get
C D = 5 1 2
A B D C = ( A C ) ( C D )
Plugging our values in...
A B D C = ( 5 ) ( 5 1 2 )
We find the area of rectangle A B D C = 1 2 .
Shortcut method:
A B D C = a b = ( 3 ) ( 4 ) = 1 2 .