The Hidden Ice Cream Cone
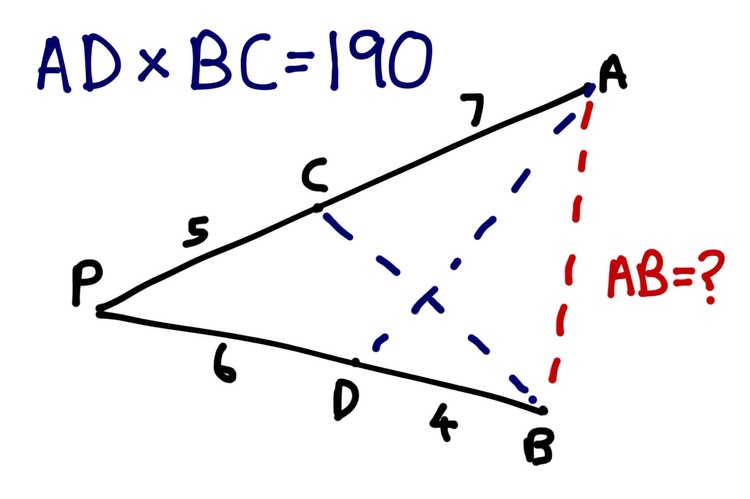 We have two intersecting lines
P
C
A
and
P
D
B
where
P
C
=
5
,
C
A
=
7
,
P
D
=
6
and
D
B
=
4
. Given that
A
D
×
B
C
=
1
9
0
, find the length of
A
B
.
We have two intersecting lines
P
C
A
and
P
D
B
where
P
C
=
5
,
C
A
=
7
,
P
D
=
6
and
D
B
=
4
. Given that
A
D
×
B
C
=
1
9
0
, find the length of
A
B
.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
I did the same as yours. This can also be done by guesswork.
Consider □ A B D B as cyclic.
Apply Ptolemy's Theorem -
A C × B D + D C × A B = B D × A C
2 8 + D C × A B = 1 9 0
D C × A B = 1 6 2
D C × A B = 2 × 9 × 9
D C × A B = 9 × 1 8
D C = 9 , A B = 1 8
Hmm, nice, I used Stewart's Theorem rather.
i want to know how you came to know that it will form a cyclic, i am still not able to understand please help me...with other solution
It's because P A × P C = P B × P D and the converse of Power of a Point states that therefore ABCD is cyclic. It is also known as intersecting chords, but the exterior version.
great job! but can you tell me what is Ptolemy's theorem?
Yes of course; Ptolemy's Theorem is a beautiful theorem about cyclic quadrilaterals. It states that if you have a cyclic quadrilateral A B C D , then A B × C D + B C × D A = A C × B D
Or in other words, the sum of the products of opposite sides is equal to the product of the diagonals. Its converse also holds and it has an amazing proof as well.
Thanks buddy!
First, we will use the Law of Cosines twice in order to find expressions for A D and B C .
Let A D = x , and B C = y . We can write the following:
x 2 = 6 2 + 1 2 2 − 2 ∗ 6 ∗ 1 2 ∗ c o s ( P )
x 2 = 6 2 ∗ ( 5 − 4 ∗ c o s ( P ) )
x = 6 ∗ 5 − 4 ∗ c o s ( P )
And also:
y 2 = 5 2 + 1 0 2 − 2 ∗ 5 ∗ 1 0 ∗ c o s ( P )
y 2 = 5 2 ∗ ( 5 − 4 ∗ c o s ( P ) )
y = 5 ∗ 5 − 4 ∗ c o s ( P )
Then, taking the product x y yields 3 0 ∗ ( 5 − 4 ∗ c o s ( P ) ) . But this value is known to be 190, thus:
3 0 ∗ ( 5 − 4 ∗ c o s ( P ) ) = 1 9 0 , which implies c o s ( P ) = − 3 1 .
Now we have everything we need to solve the problem.
Let A B = z . Applying the Law of Cosines one last time will yield the following:
z 2 = 1 0 2 + 1 2 2 − 2 ∗ 1 0 ∗ 1 2 ∗ c o s ( P )
z 2 = 1 0 0 + 1 4 4 + 8 0 = 3 2 4
z = 1 8 which is the answer sought.
Solution using Co-ordinate geometry.

Applying the converse of the Power of a Point theorem shows that A B D C is cyclic. (That's why it looks a bit like an ice cream with its cone when you add the circle.)
Also note that by SAS similarity P C D ~ P B A . So A B = 2 C D .
Now by Ptolemy's Theorem, 7 × 4 + 2 C D 2 = 1 9 0 and it follows that C D = 9 ⟹ A B = 1 8 as required.