The hunter and the monkey
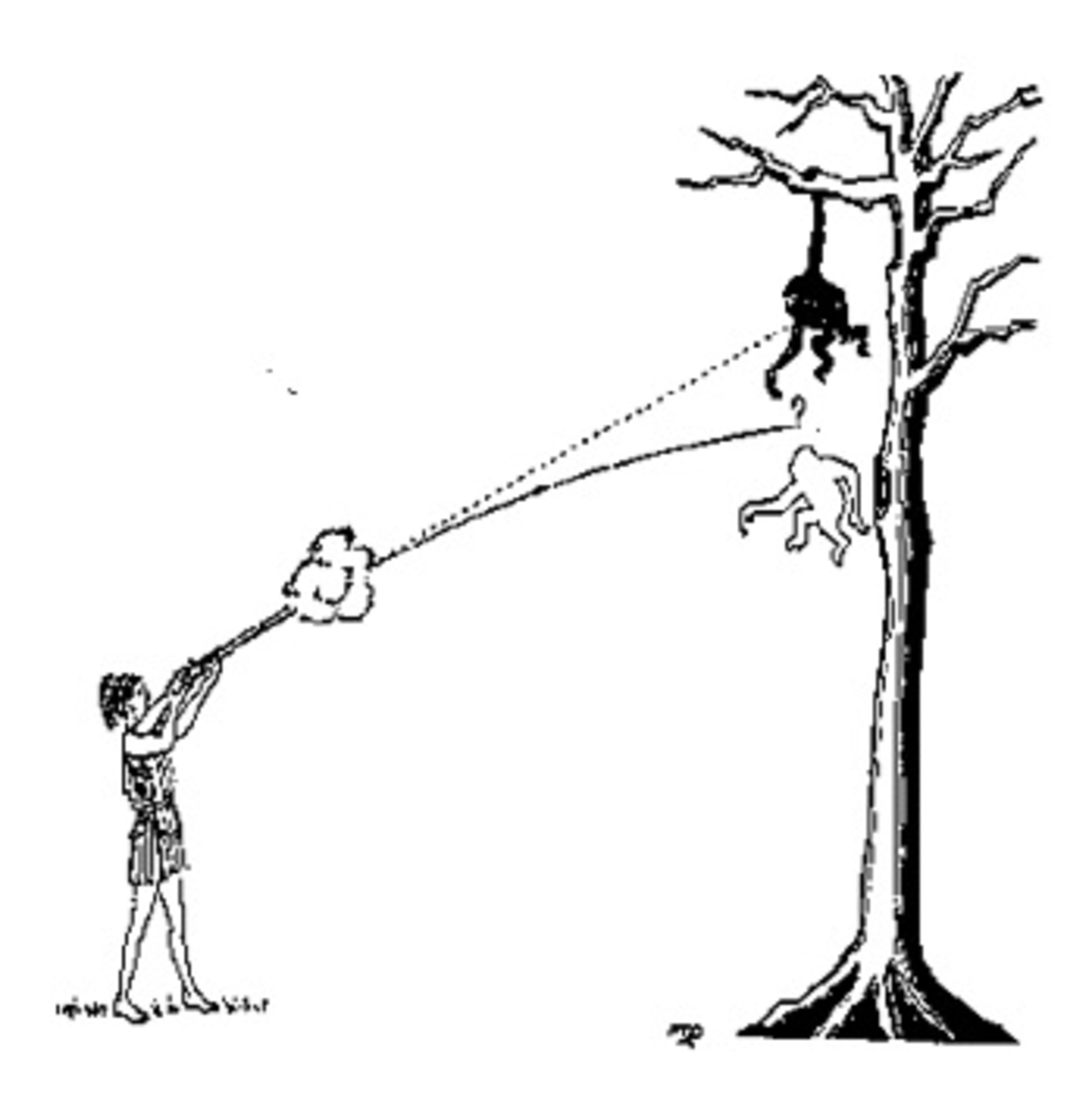
A hunter shoots a sedative dart at a mischievous monkey that hangs from a tree branch after having escaped from his cage. The monkey--that ignores the laws of physics--releases himself from the branch right at the moment he hears the shot.
When jumping, can the monkey avoid being hit by the sedative dart?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the monkey simply lets go, it will be hit by the dart. But if he jumps with sufficiently large velocity component perpendiular to the line of fire, the dart will miss.
To analyze this, consider that the motions of monkey and dart are described as x m = x m , 0 + v m , 0 t + 2 1 g t 2 ; x d = x d , 0 + v d , 0 t + 2 1 g t 2 . Moreover, v d , 0 is directed toward the monkey, so that v m , 0 − v d , 0 = v d , 0 t 0 .
Subtracting the two equations and using this substitution, we find x m − x d = v d , 0 ( t 0 − t ) + v m , 0 t . The monkey is hit if this expression every becomes zero. Obviously, if the second term v m , 0 is not parallel to the vector v d , 0 , this will never be the case.
On the other hand, if v m , 0 = α v d , 0 is parallel to the direction in which the dart is launched, the equation becomes v d , 0 ( t 0 + ( 1 − α ) t ) = 0 , so that the monkey will be hit at time t = t 0 / ( 1 − α ) . (There is no positive solution, i.e. no hit, if α ≥ 1 . This means that the monkey launches itself in the same direction as the dart, but at a higher speed!)