The impatient boatman
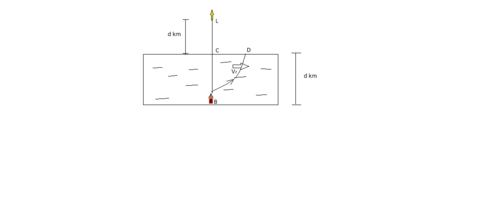 There is a river of width 'd' km,on one side of which is an impatient boatman B,who wants to reach the lighthouse L which is exactly opposite him and'd' km further from the opposite bank as shown in the figure.
There is a river of width 'd' km,on one side of which is an impatient boatman B,who wants to reach the lighthouse L which is exactly opposite him and'd' km further from the opposite bank as shown in the figure.
So he hires a speedboat which has speed' v B '(in still water) equal to that of the river ' v r ' .
He reckons that to reach there in the shortest time , his boat should always point towards the lighthouse.He reaches the opposite bank at D.
Find distance CD(in km).
Details and Assumptions
→ v r =5 km/hr
→ d=1km
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
At any point in the trajectory of the boat,let the line joining it and the lighthouse BL make an angle 180- θ with the direction of river current.As the boatman tries to point the boat towards the lighthouse,velocity of boat w.r.t river v B , R at any time, will be along the line joining the boat and the light house.
if we find net component of velocity of the boat along this line at any time, v B L ,we get
v B L = v B , R − v R . c o s ( θ ) = v R − v R . c o s ( θ ) ∵ v R = v B , R
this is same in magnitude as the net component of velocity of the boat along the river current, v x
v x = v R − v B , R . c o s ( θ ) = v R − v R . c o s ( θ )
∴ Distance traveled towards lighthouse=Distance traveled along the river.
∴ CD=(2 × d)-DL
Let CD='x'km Applying pythagoras theorem in Δ LCD, We get x=3 × d/4 Putting values, we get x=0.75
I solved this question by the concept of relative velocity.
Let A be the final position of the boat. Any general position of the boat is shown in the figure.
Velocity of approach of the boat to the light house is v − v c o s θ
So − d t d a = ( v − v c o s θ )
On setting the limits we get
− ∫ 2 d x 2 + d 2 d a = ∫ 0 T ( v − v c o s θ ) d t ......................(1)
Now in this time interval the would cover x km in horizontal direction
So d t d s = ( v − v c o s θ )
On setting the limits we get
∫ 0 x d s = ∫ 0 T ( v − v c o s θ ) d t ........(2)
The term in the LHS of 1st equation and RHS of second equation is same. So eliminating that term we get
x = 4 3 d . On putting values we get x = 0 . 7 5