The Knights Dilemma
 What is the maximum number of knights you can place on a
chessboard such that no two of them attack each other?
What is the maximum number of knights you can place on a
chessboard such that no two of them attack each other?
Details and assumptions
-
The knights are placed on distinct cells.
-
Two knights attack each other if they are one cell vertically and two cells horizontally apart or two cells vertically and one cell horizontally apart.
-
A chessboard has cells.
-
Here's an example of knights being placed on a chessboard which attack each other.
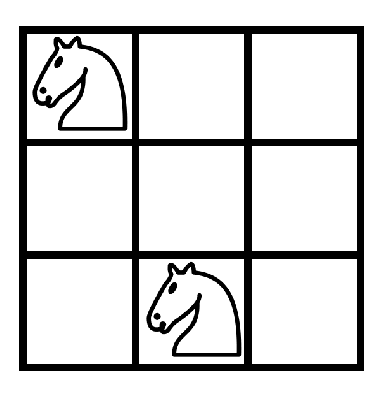
Image credit: Wikipedia
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can divide the chessboard into 32 groups each with two squares(I only coloured 8 groups, you can colour the rest using the same pattern.) such that the squares are a knight's move away.
Let the number of knights that can be placed be n . If n > 3 2 , then by PHP, two knights must be in the same group. But then they will attack each other. Therefore n ≤ 3 2 . To prove that n = 3 2 is the maximum, we must find a configuration of 32 knights.
Note that a knight always attacks squares of a different color.(i.e. if its on a black square, it attacks only white squares.) Therefore, if we put all the knights on squares of the same color(WLOG black), then they will not be able to attack each other. Total number of black squares = 32.
Therefore the maximum number of knights which can be placed on a 8X8 chessboard so that they do not attack each other is 3 2 .