The Koninsberg Bridge Problem
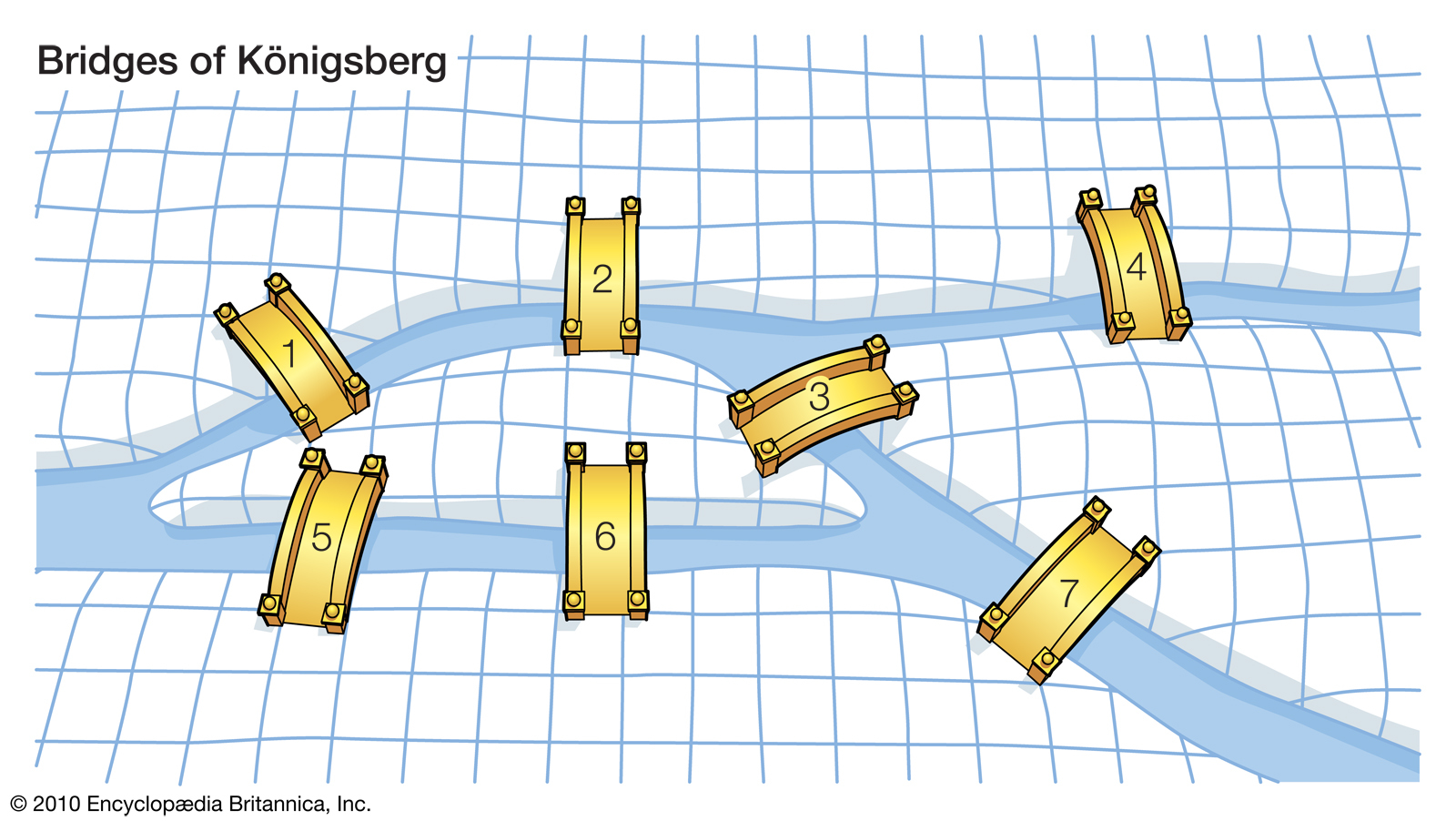
It is set in Koninsberg, now Kaliningrad, Russia. The river Pregel runs through Koninsberg, and on it are two islands - Kneiphof and Lomse. Those bridges were connected to the mainland and each other by 7 bridges. You can see those in the image above. Eventually, locals started wondering if you could cross each bridge once and only once. You are allowed to end your route either on an island or on the mainland.
Details:
- You can only get to the mainland or an island via a bridge.
- Crossing only counts if you cross the bridge. You can not backtrack on a bridge midway.
Is crossing each bridge only once possible?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a 4-partite graph and it is well known that a connected graph has an Eulerian path if and only if it has exactly 2 vertices of odd degree . Here, we have 4 vertices of odd degree, thus, you cannot cross each bridge only once.