The largest circle

The largest circle inscribed in the triangle is its incircle with its centre having equal perpendicular distances, its radius $r$ , to the three sides (see figure above).

Therefore, the area of the triangle is given by $A = \frac 12 (a+b+c)r$ , where $a$ , $b$ and $c$ are the sides lengths of the triangle. And by Heron's formula we have $A=\sqrt{s(s-a)(s-b)(s-c)}$ , where $s=\dfrac {a+b+c}2$ . Therefore, we have:

$\begin{aligned} \frac {(a+b+c)r}2 & = \sqrt{s(s-a)(s-b)(s-c)} \\ sr & = \sqrt{s(s-a)(s-b)(s-c)} \\ \implies r & = \sqrt{\frac {(s-a)(s-b)(s-c)}s} & \small \color{#3D99F6} \text{Note that }a=3, b=5, c=6, \implies s = 7 \\ & = \sqrt{\frac {(7-3)(7-5)(7-6)}7} \\ & = \sqrt{\frac 87} \end{aligned}$

Therefore, the area of the incircle $A_\circ = \pi r^2 = \frac 87 \pi$ . $\implies a+b = 8+7 = \boxed{15}$

Relevant wiki: Incircle of Triangle

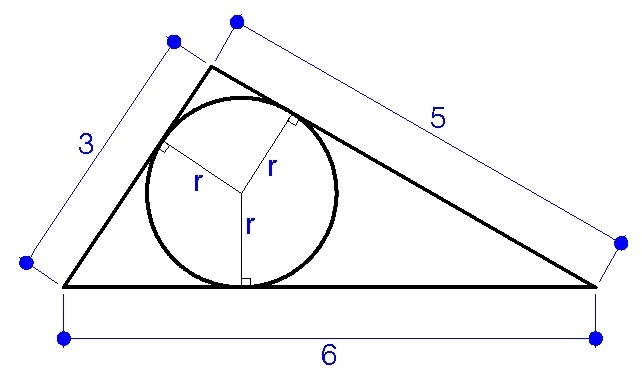
The radius of the incircle is given by the formula $\boxed{r=\dfrac{2A}{P}}$ where: $A$ = area of the triangle and $P$ = perimeter of the triangle

The area of the triangle can be computed using the Heron's Formula , $A=\sqrt{s(s-a)(s-b)(s-c)}$ where: $s$ = semi-perimeter of the triangle, $a,b,c$ = side lengths of the triangle

$s=\dfrac{3+5+6}{2}=7$

$A=\sqrt{7(7-3)(7-5)(7-6)}=\sqrt{56}=2\sqrt{14}$

$P=3+5+6=14$

Computing for the radius of the incircle, we have

$r=\dfrac{2(2\sqrt{14})}{14}=\dfrac{2\sqrt{14}}{7}$

Computing for the area of the incircle, we have

$A=\pi r^2=\pi\left(\dfrac{2\sqrt{14}}{7}\right)^2=\pi \left[\dfrac{4(14)}{49}\right]=\pi \left(\dfrac{56}{49}\right)=\dfrac{8}{7}\pi$

Finally,

$a+b=8+7=$ $\color{#3D99F6}\large\boxed{15}$ $\boxed{\text{answer}}$