The leaking container
A body of water is contained in a spherical container with diameter 0.6 meter. Suddenly, it gets leaked by a circular hole at the lowest point (the hole is 0.3 meter below center). The hole's diameter is 0.006 meter. The drawing below is not to scale.
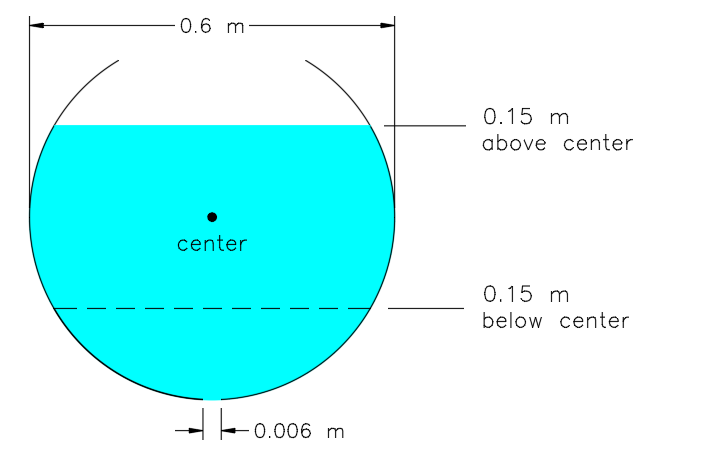
How long does it take in seconds for water to fall from 0.15 m above center to 0.15 m below center?
Submit the answer as the first 5 significant figures of your result. For example, submit 78940 if you get 78.94067, submit 94084 if you get 940.84058, etc.
Details and assumptions:
Gravitational acceleration g = 9 . 8 1 m / s 2
The fluid is incompressible, so the volume flow rate is constant at all positions.
Ignore factors such as friction, minor losses, surface tension, etc. so that the flow obeys Bernoulli's equation :
P A + 2 1 ρ v A 2 + ρ g h A = P B + 2 1 ρ v B 2 + ρ g h B
Both the water surface and the hole are exposed to open atmosphere.
Though technically, the circular hole will distort the container's shape, making it no longer a sphere and the hole's distance to center is less than 0.3 m. But for simplicity, assume the water inside is always part of a perfect sphere and the hole is exactly 0.3 m below center.
Note:
My solution involves a bit of programming to get through a hard part. If you can solve this manually, please tell me below. Thank you.
The answer is 11704.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution! However ( although apparently it is insignificant ), it should be mentioned that the kinetic head at the surface is taken to be negligible v B ≈ 0 in your solution. I accounted for it, then trying to be cute, linearized it around R . I ended up at 1263.5 s ( in both accounting for it and ignoring it) . I suppose the linearization wasn't as smart a move as anticipated...
Torricelli's Law is a consequence of Bernoulli's principle, and it is useful here (second line of math below). In addition to the parameters already defined in the problem, let a be the cross-sectional area of the hole, let h be the height of the water above the hole, let u be the flow speed at the hole, let y be the height of the water above the sphere center, and let V be the volume of water in the sphere. Conceptualize the infinitesimal change in volume d V as a cylinder of water at the surface, with height d y and radius x = R 2 − y 2 .
h = y − ( − R ) u = 2 g h d t d V = − a u d V = π x 2 d y = π ( R 2 − y 2 ) d y d t π ( R 2 − y 2 ) d y = − a u d y = π ( R 2 − y 2 ) − a u d t
I numerically integrated d y to arrive at a final time of ≈ 1 1 7 0 . 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
|
This is much simpler than my solution. Thank you. I forgot that I can use Torricelli's Law here.
Let the water surface be point A, the hole be point B, the datum is at the sphere's center. See the picture below:
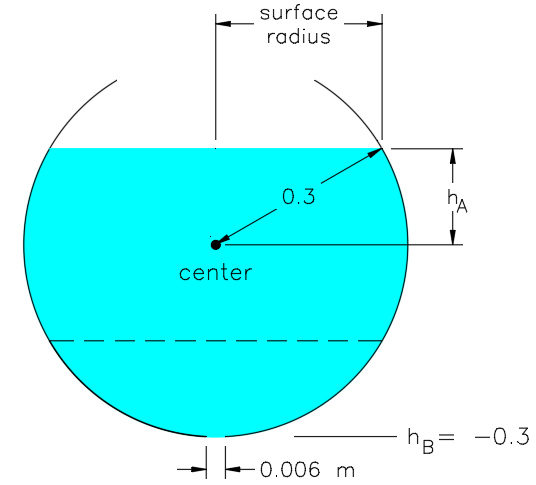
Surface is a circle with area: A A = π ( 0 . 3 2 − h A 2 )
Hole area: A B = π 0 . 0 0 3 2
Volume flow rate is constant, so: A A v A = A B v B
≡ v A v B = 0 . 0 0 3 2 0 . 3 2 − h A 2
Substituting this into Bernoulli's equation gives: 2 v A 2 + g h A = − 0 . 3 g + 0 . 0 0 3 4 ( 0 . 3 2 − h A 2 ) 2 v A 2 (Gauge pressure at both points is 0, then you can cancel density)
A bit of algebraic manipulations give v A = − 2 g 0 . 0 0 3 4 ( 0 . 3 2 − h A 2 ) 2 − 1 h A + 0 . 3 (water level is going down so it's negative)
The rest is calculus:
v A = d t d h A
≡ d t = v A d h A
≡ t = ∫ h = 0 . 1 5 h = − 0 . 1 5 v d h
≡ t = − ∫ h = − 0 . 1 5 h = 0 . 1 5 v d h
Now you basically solve this integral and get answer:
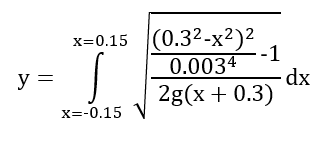
(I changed the variables so it's easier to see)
Now if you can solve this by hand, please tell me. I had to use Simpson's rule and programming.
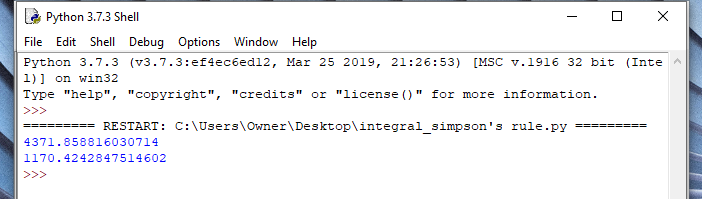
Put these codes into python:
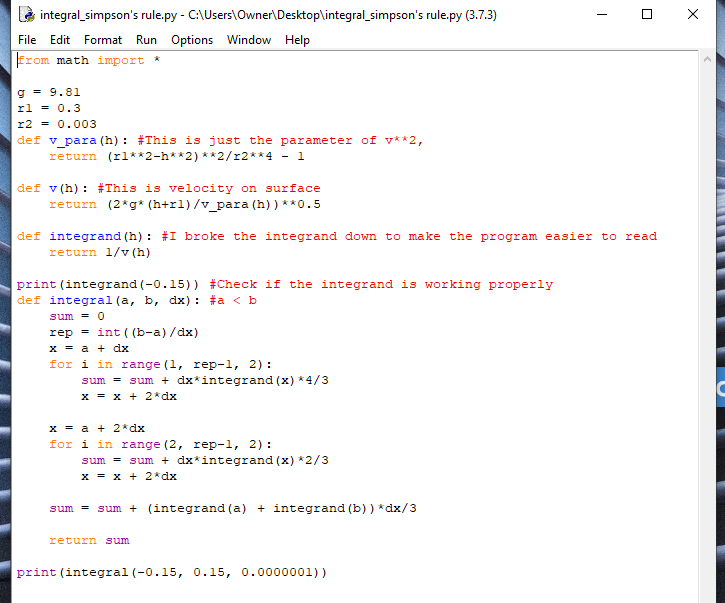
The program gives 1170.42... so the answer is 11704.
If h is the height of the water level above the bottom of the sphere, and V the volume of water, then we have V = 3 1 π h 2 ( 3 R − h ) where R is the radius of the container, and Bernoulli's Principle tells us that V ˙ = − π r 2 2 g h where r is the radius of the outflow. Thus π h ( 2 R − h ) h ˙ h ( 2 R − h ) h ˙ = V ˙ = − π r 2 2 g h = − r 2 2 g and so, if T is the time for the water level to drop from 2 1 R above the centre of the sphere to 2 1 R below the centre, then T = ∫ 2 1 R 2 3 R r 2 2 g h ( 2 R − h ) d h = r 2 2 g R 2 5 ∫ 2 1 2 3 k ( 2 − k ) d k = 6 0 3 3 3 − 1 7 ( r R ) 2 g R With R = 0 . 3 , r = 0 . 0 0 3 , g = 9 . 8 1 we deduce that T = 1 1 7 0 . 4 2 4 6 2 8 seconds, giving the answer 1 1 7 0 4 .