The length of the square
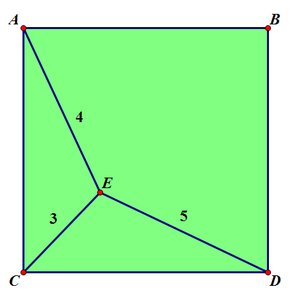 Point
E
in square
A
B
C
D
is such that
C
E
=
3
,
A
E
=
4
, and
D
E
=
5
. Find the side length of square
A
B
C
D
. Round your answer to four decimal places.
Point
E
in square
A
B
C
D
is such that
C
E
=
3
,
A
E
=
4
, and
D
E
=
5
. Find the side length of square
A
B
C
D
. Round your answer to four decimal places.
The answer is 6.0715.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
If triangle CEE' is an isosceles right triangle, then CE is a section of the disgonal CB. Now if you put any point on the diagonal CB ( in this case point E ) lengths AE and DE are supposed to be congruent. In your case AE =4 and DE = 5 which they're not congruent.
Log in to reply
If triangle CEE' is an isosceles right triangle, then CE is a section of the disgonal CB.
I think that's wrong.
Let the side length of square A B C D be a , Let the coordinates be C ( 0 , 0 ) , A ( 0 , a ) , D ( a , 0 ) , and E ( x , y ) . By Pythagorean theorem , we have:
⎩ ⎪ ⎨ ⎪ ⎧ C E : A E : D E : x 2 + y 2 = 9 x 2 + ( y − a ) 2 = 1 6 ( x − a ) 2 + y 2 = 2 5 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From ( 2 ) − ( 1 ) : a 2 − 2 a y = 7 ⟹ y = 2 a a 2 − 7 . Similarly, from ( 3 ) − ( 1 ) : ⟹ x = 2 a a 2 − 1 6 . As ( 1 ) : x 2 + y 2 = 9 , we have:
( 2 a a 2 − 7 ) 2 + ( 2 a a 2 − 1 6 ) 2 2 a 4 − 4 6 a 2 + 3 0 5 2 a 4 − 8 2 a 2 + 3 0 5 = 9 = 3 6 a 2 = 0
⟹ a 2 ⟹ a = 4 8 2 + 8 2 2 − 4 ( 2 ) ( 3 0 5 ) = 2 4 1 + 3 1 1 9 ≈ 6 . 0 7 1 5
Wow, your idea is much simpler than mine!
Log in to reply
Yes, glad that you like it.
Log in to reply
Yes I like it very much! I used to search for a long time to find my solution, but it is not as concise as your solution!
I love your problem solving
Log in to reply
Glad that you like it. Upvote the my solution if you have not.
Let x = A C = C D , θ = ∠ A C E , and y = cos θ .
By the law of cosines on △ A C E , 4 2 = 3 2 + x 2 − 2 ⋅ 3 ⋅ x ⋅ cos θ = 9 + x 2 − 6 x y , which rearranges to 3 6 x 2 y 2 = x 4 − 1 4 x 2 + 4 9 .
By the law of cosines on △ E C D , 5 2 = 3 2 + x 2 − 2 ⋅ 3 ⋅ x ⋅ cos ( 9 0 ° − θ ) = 9 + x 2 − 6 x sin θ = 9 + x 2 − 6 x 1 − cos 2 θ = 9 + x 2 − 6 x 1 − y 2 , which rearranges to 3 6 x 2 y 2 = − x 4 + 6 8 x 2 − 2 5 6 .
Therefore, 3 6 x 2 y 2 = x 4 − 1 4 x 2 + 4 9 = − x 4 + 6 8 x 2 − 2 5 6 , so 2 x 4 − 8 2 x 2 + 3 0 5 = 0 , which solves to x = 2 4 1 + 3 1 1 9 ≈ 6 . 0 7 1 5 for x > 0 .
Let z be size of square and write the following three relations:
(1). x^2+y^2=3^2
(2). x^2+(z-y)^2=4^2
(3). y^2+(z-x)^2=5^2
Solve with WolframAlpha
Answer z~=6.0715
Rotate triangle ACE 90 degrees clockwise to get triangle DCE',connect the EE' and AD,extended AE intersects DE' at F.We can get the following information:
The triangle CEE' is an isosceles right triangle.So EE' is going to be equal to 3 2 .
D E ′ = A E = 4 .
A E ⊥ D E ′ (AE rotates 90 degrees through the triangle ACE to become DE', so they're perpendicular.).
The first solution:Crazy use of the Pythagorean theorem
Let's focus on the triangle DEE'.Let's say FD is x ,so:
E E ′ 2 − E ′ F 2 = D E 2 − D F 2
1 8 − ( 4 − x ) 2 = 2 5 − x 2
x = 8 2 3
So DF is equal to 8 2 3 , and then we get EF is equal to D E 2 − D F 2 ,which is 8 1 0 7 1 .
So we can figure out that AD is equal to A F 2 + D F 2 , which is 6 4 2 6 2 4 + 6 4 1 0 7 1 (This number looks terrible).
And we also know that the sum of the squares of the two sides of the square is equal to the square of the diagonal, so the length of the sides of the square is equal to 2 1 of the diagonal,which is A B = 2 1 A D .
So the side length is
1 2 8 2 6 2 4 + 6 4 1 0 7 1 ≈ 6 . 0 7 1 5
The second solution:Cosine formulas
Cosine formula:
c 2 = a 2 + b 2 − 2 a b cos C
C = cos − 1 ( 2 a b a 2 + b 2 − c 2 )
In triangle DEE', we get the degree of Angle DE'E by using the second formula:
∠ D E E ′ = cos − 1 ( 2 × 3 2 × 4 2 × 3 2 + 4 2 − 5 2 ) ≈ 7 4 . 6 2 3 ∘
And because the triangle CEE' is a right-angled isosceles triangle, the angle CE'E is equal to 45 degrees, so the angle CE'D is approximately equal to 119.623 degrees.
And then you apply the first formula:
C D 2 = 3 2 + 4 2 − 2 × 3 × 4 × cos ( 1 1 9 . 6 2 3 ∘ )
So you compute this, and you get:
C D = A B ≈ 6 . 0 7 1 5
T i p : I f I h a v e a n y m i s t a k e s i n m y p r o c e s s , p l e a s e c o r r e c t t h e m i n t h e c o m m e n t s s e c t i o n . T h a n k y o u !