The Logistic Function (Population Growth)
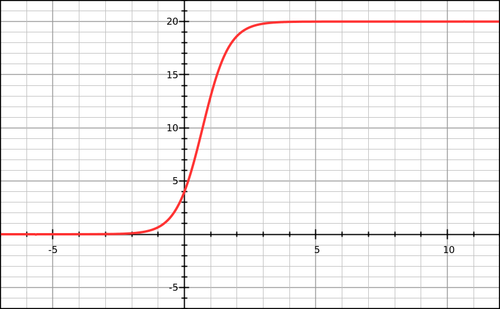 Exponential functions are prevalent in many problems in science, business, economics, medicine, and sociology. One important function, the logistic function, is often used to analyze population growth that is limited by natural environmental factors. The general form of the logistic function is
Exponential functions are prevalent in many problems in science, business, economics, medicine, and sociology. One important function, the logistic function, is often used to analyze population growth that is limited by natural environmental factors. The general form of the logistic function is
where constants , , and are usually determined experimentally.
Suppose that population in a town is modeled by
where is number of population and is time in year. Let be the time when the population growth rate begin to decline and be the time when the population reach percent of its limit, then can be expressed as . Determine the value of .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The population growth rate is given by P ′ ( t ) = ( 1 + B e − C t ) 2 A B C e − C t and the population acceleration rate is given by P ′ ′ ( t ) = ( 1 + B e − C t ) 3 A B 2 C 2 e − 2 C t − A B C 2 e − C t Since lim t → ∞ P ( t ) = A , putting P ( t ) = 5 4 A , we get t 2 = 2 l g 2 and putting P ′ ′ ( t ) ≤ 0 gives us t 1 ≥ l g 2