THE LONELY ANGLE...
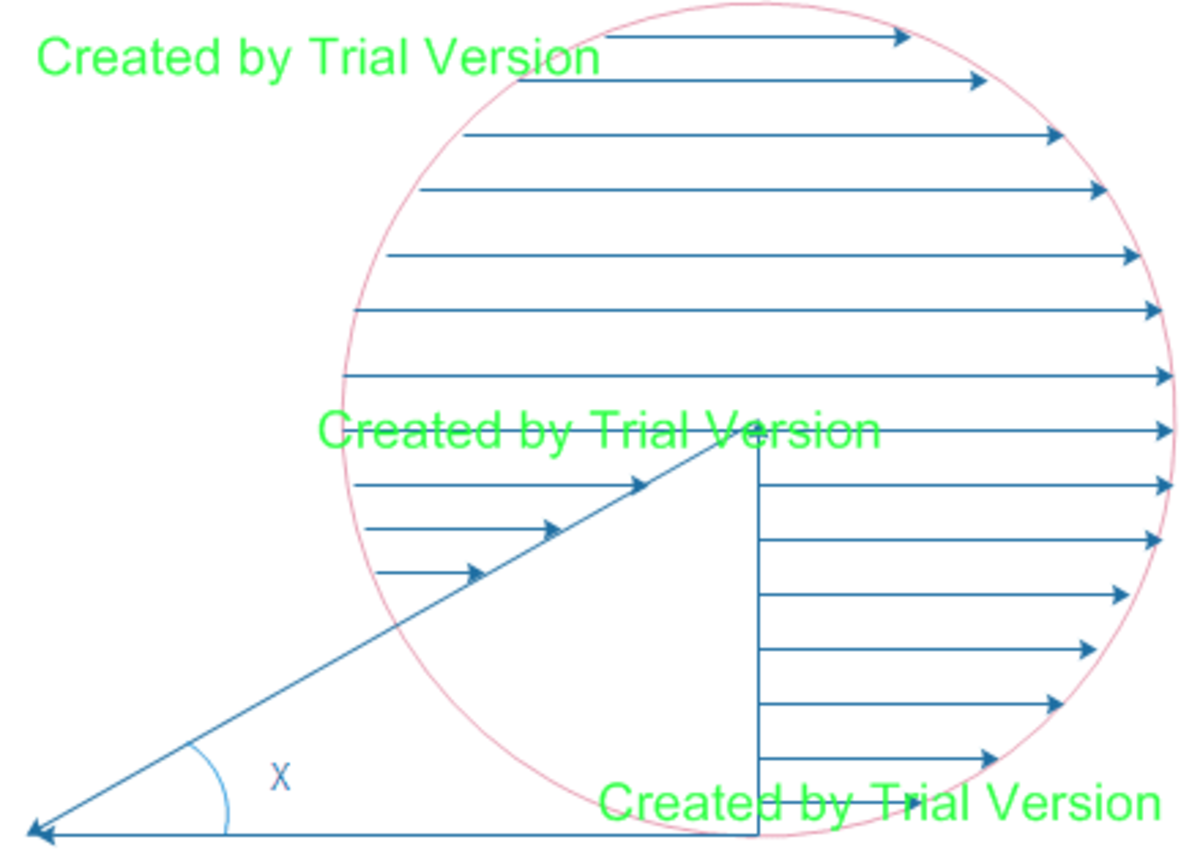
The above circle has a radius of 4 units. If the area of the shaded region is 14 pi then what is the value of angle X in degrees ..??
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Area of unshaded region is pi (4^2)=16pi-14pi=2pi,and we know (angle/360)pir^2=2pi so angle=45,that means x=90-45=45(as its a right triangle)
We will assume that the topmost vertex of the triangle is at the center of the circle, and that the base of the triangle is tangent to the circle. We are thus dealing with a right-angled triangle, so x will be the complement of θ , where θ is the uppermost angle of the triangle.
Since the area of the entire circle is 1 6 π , the area of the unshaded sector is 1 6 π − 1 4 π = 2 π . The area of the unshaded sector is also given by the formula 2 1 ∗ r 2 ∗ θ , where θ is in radians. So with r = 4 we have that
2 1 ∗ 1 6 ∗ θ = 2 π ⟹ θ = 4 π radians = 4 5 degrees.
So finally we have x = 9 0 − θ = 4 5 degrees.
Area of full circle is 16 pi square units
Shaded area is 7/8 of full circle (14 pi/16 pi square units)
So 1/8 of the complete circle is unshaded.
Triangle is a right angled triangle, so the angle at the circle's centre must be 1/8 of 360 degrees, i.e. 45 degrees
x therefore must also be 45 degrees