The loop problem!

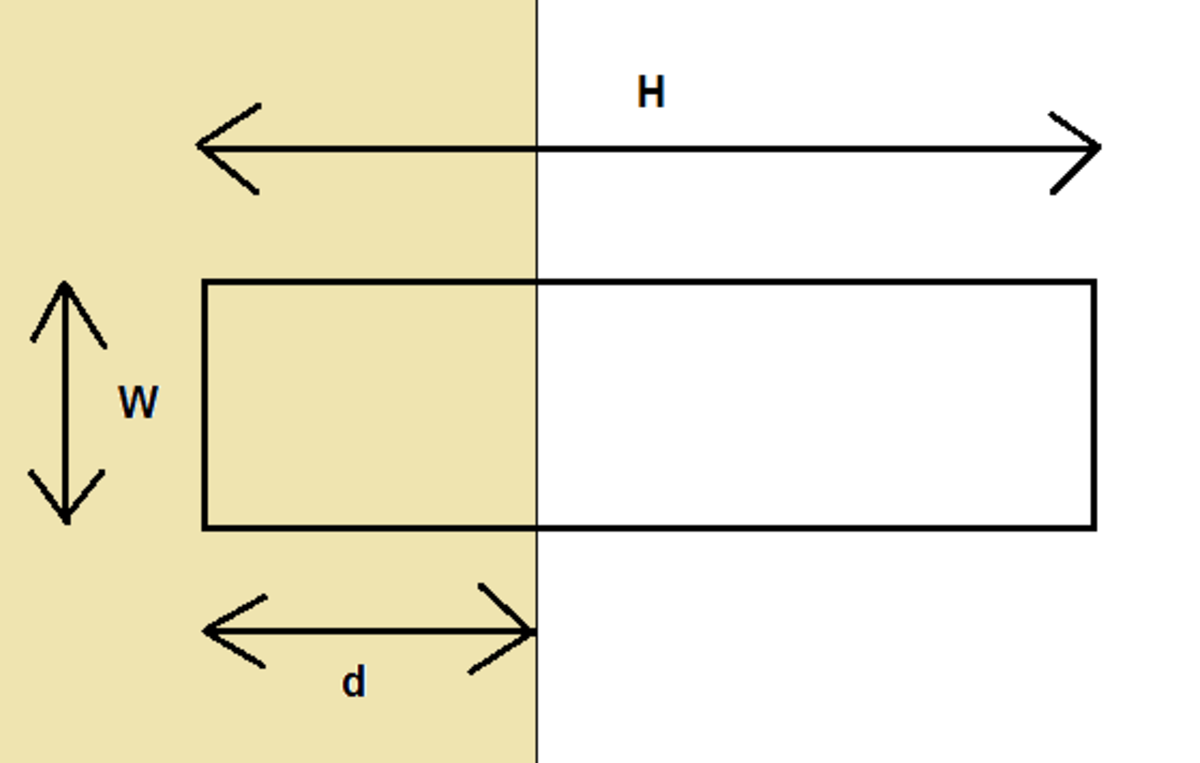
The loop becomes to move because of induction. A changing magnetic field produces an EMF to the loop which causes current to flow.The external magnetic field produces a force to the current carrying wire. The EMF induced in the loop is $U$ = $-d\phi/dt$ = - $A_l$ $dB/dt$

where $A_l$ = $ld$

The current is $I = U/R$ where

$R = \sigma s/A_w$

with $s=2l +2h$ , $A_w$ is the cross sectional area of the wire and $\sigma$ is the resitivity of copper.

Thus $I = U/R$ = $[A_l (dB/dt) A_w]/\sigma s$ = $0.0705 A$

The net force exerted by the magnetic field is $F = BIl$ and the acceleration is $a = F/m$

= $[A_l (dB/dt) A_w]/\sigma s^2 p$

= $0.627 m/s^2$

Thus $a = 0.63 m/s^2$ .

I used a slightly different naming convention, as shown in the diagram.

The most efficient way to do a problem like this is with a spreadsheet or programming script. Python script below:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

import math

cu_dens = 8940.0                # copper mass density
rho_cu = 1.68 * (10.0**-8.0)    # copper resistivity

W = 0.1                         # Loop short side length
H = 0.3                         # Loop long side length
L = 2.0*(W+H)                   # Total loop length
r = 0.001                       # Wire radius
Bdot = 0.025                    # B rate of change
B0 = 2.0                        # Initial B value
d = 0.12                        # Initial penetration into B region

Across = math.pi * (r**2.0)     # Wire cross-sectional area
Vol_cu = Across * L             # Loop copper volume
m_cu = Vol_cu * cu_dens         # Loop copper mass      

R = rho_cu * L / Across         # Total loop resistance

Vind = Bdot * W*d               # Voltage induced

I = Vind / R                    # Loop current

F = I*W*B0                      # Magnetic force on loop

acc = F / m_cu                  # Loop acceleration

print acc

# Answer is 0.624201022691