The Louvre
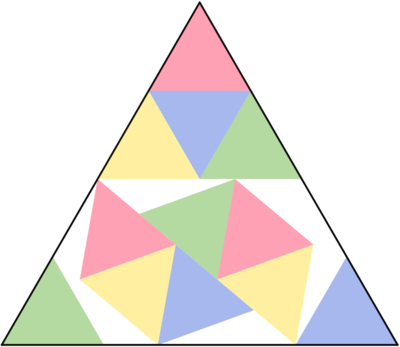
The figure shows twelve identical unit equilateral triangles packed inside a bigger equilateral triangle.
The side length of the bigger equilateral triangle is 2 + 2 cos θ .
Find θ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
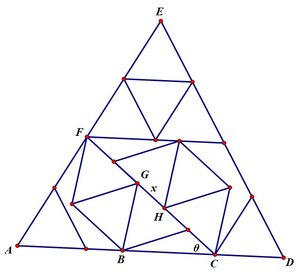 Suppose that the length
G
H
=
x
, and that
∠
A
C
F
=
θ
. Applying the Sine Rule to the triangle
B
C
G
, we see that
(
1
+
x
)
sin
θ
=
sin
(
1
2
0
∘
−
θ
)
If
X
is the length of the large equilateral triangle, then
X
=
1
+
A
C
=
1
+
sin
6
0
∘
(
2
+
x
)
sin
(
1
2
0
∘
−
θ
)
using the Sine Rule on
A
C
F
. On the other hand
X
=
2
+
A
F
=
2
+
sin
6
0
∘
(
2
+
x
)
sin
θ
Putting these last equations together,
sin
6
0
∘
=
(
2
+
x
)
[
sin
(
1
2
0
∘
−
θ
)
−
sin
θ
]
=
(
2
+
x
)
sin
(
6
0
∘
−
θ
)
and hence we obtain the equation
sin
(
6
0
∘
−
θ
)
sin
6
0
∘
sin
6
0
∘
sin
θ
sin
θ
=
2
+
x
=
sin
θ
sin
(
1
2
0
∘
−
θ
)
+
1
=
sin
θ
sin
(
6
0
∘
+
θ
)
+
1
=
sin
(
6
0
∘
−
θ
)
sin
(
6
0
∘
+
θ
)
+
sin
θ
sin
(
6
0
∘
−
θ
)
=
4
3
cos
2
θ
+
4
1
3
sin
2
θ
=
sin
(
2
θ
+
6
0
∘
)
and hence we have
2
θ
+
6
0
∘
=
1
8
0
∘
−
θ
, and hence
θ
=
4
0
∘
. From this we can now calculate that
x
=
2
1
sec
2
0
∘
and that
X
=
2
+
2
cos
2
0
∘
, making the answer
2
0
∘
.
Suppose that the length
G
H
=
x
, and that
∠
A
C
F
=
θ
. Applying the Sine Rule to the triangle
B
C
G
, we see that
(
1
+
x
)
sin
θ
=
sin
(
1
2
0
∘
−
θ
)
If
X
is the length of the large equilateral triangle, then
X
=
1
+
A
C
=
1
+
sin
6
0
∘
(
2
+
x
)
sin
(
1
2
0
∘
−
θ
)
using the Sine Rule on
A
C
F
. On the other hand
X
=
2
+
A
F
=
2
+
sin
6
0
∘
(
2
+
x
)
sin
θ
Putting these last equations together,
sin
6
0
∘
=
(
2
+
x
)
[
sin
(
1
2
0
∘
−
θ
)
−
sin
θ
]
=
(
2
+
x
)
sin
(
6
0
∘
−
θ
)
and hence we obtain the equation
sin
(
6
0
∘
−
θ
)
sin
6
0
∘
sin
6
0
∘
sin
θ
sin
θ
=
2
+
x
=
sin
θ
sin
(
1
2
0
∘
−
θ
)
+
1
=
sin
θ
sin
(
6
0
∘
+
θ
)
+
1
=
sin
(
6
0
∘
−
θ
)
sin
(
6
0
∘
+
θ
)
+
sin
θ
sin
(
6
0
∘
−
θ
)
=
4
3
cos
2
θ
+
4
1
3
sin
2
θ
=
sin
(
2
θ
+
6
0
∘
)
and hence we have
2
θ
+
6
0
∘
=
1
8
0
∘
−
θ
, and hence
θ
=
4
0
∘
. From this we can now calculate that
x
=
2
1
sec
2
0
∘
and that
X
=
2
+
2
cos
2
0
∘
, making the answer
2
0
∘
.
Better than my solution, which was an ultimate trig bash that took me 30 minutes.