The Lucky Thief
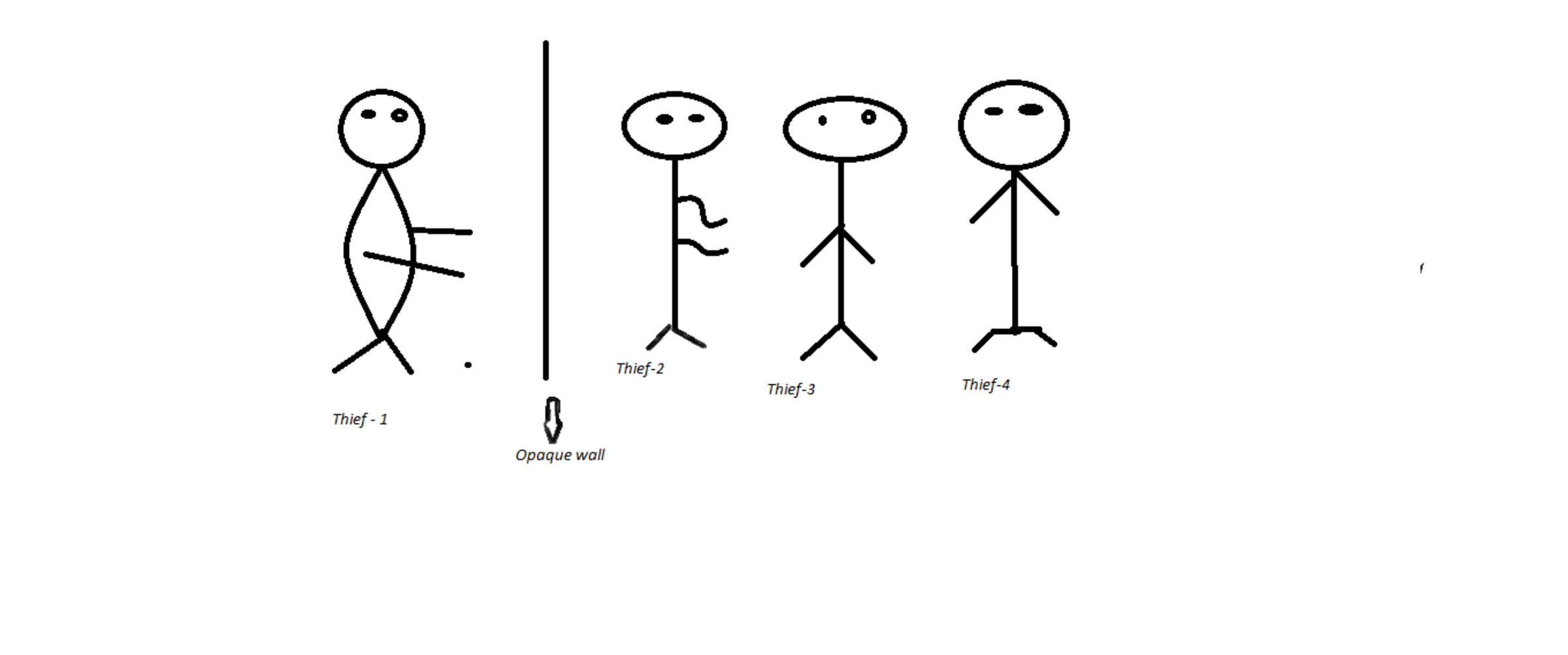
On the ocasion of teachers day police orders to release one theif .The officer had caps , white and black[Caps are distributed in such a way that no two caps of same color are together].The first theif who tells the right cap (color) "he" is wearing will be relesed , the situation is such that theif 2 cannot answer then find the theif that will be released.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I think the question stated here is not correctly stated. I answered it because i did not find any button to report this. I must say that many times ago i read a puzzle like this. if i am not wrong, this question is copied from somewhere or slightly modified. But that's not a big problem, the problem is that i think Kritarth Lohomi omitted few important condition to mention so that the problem becomes soluble. The following is the correct question i think (I copied it from a site). .
*4 MEN IN HATS
*
They can’t move – they can only look forward. Between A and B is a brick wall which is completely opaque (they absolutely can’t see through it). They are all aware that each of them is wearing a hat, and that two of them are wearing a black hat, and two of them are wearing a white hat. They don’t know what color THEY are wearing. However, each of them DOES know where the other three are buried.
In order to avoid being executed, one of them must call out to the executioner the color of their hat. If they get it wrong, everyone will be shot. They can’t talk to each other and have only 10 minutes to figure it out.
After 60 seconds, one of them calls out. QUESTION: Which one of them calls out? How can he be certain he knows the color of his hat? This is not a silly trick question.
There’s no outside influence and no other way of communicating.
They can’t move and are buried in a straight line; A and B can only see their respective sides of the wall, C can see B, and D can see B and C. Here’s the answer:
C calls out that he is wearing a black hat.
He’s 100% certain because D can’t answer, and neither can A or B.
D can see C and B, but can’t determine his own hat color. B can’t see anyone and also can’t determine his own hat color. A is in the same situation as B, where he can’t see anyone and can’t determine his own hat color.
Since A, B, and D are silent, that leaves C. C knows he is wearing a black hat because if D saw that both B and C weer wearing white hats, then he would have answered. But since D is silent, C knows that he must be wearing a black hat as he can see that B is wearing a white hat.