The magic square legend

According to a legend , there was at one time in ancient China a huge flood. While the great king Yu was trying to channel the water out to sea, a turtle emerged from it with a curious pattern on its shell (see the image below): a magic square, i.e. a $nxn$ square grid filled with distinct positive integers in the range $1,2,...,n^2$ such that each cell contains a different integer and the sum $x$ of the integers in each row, column and diagonal is equal. 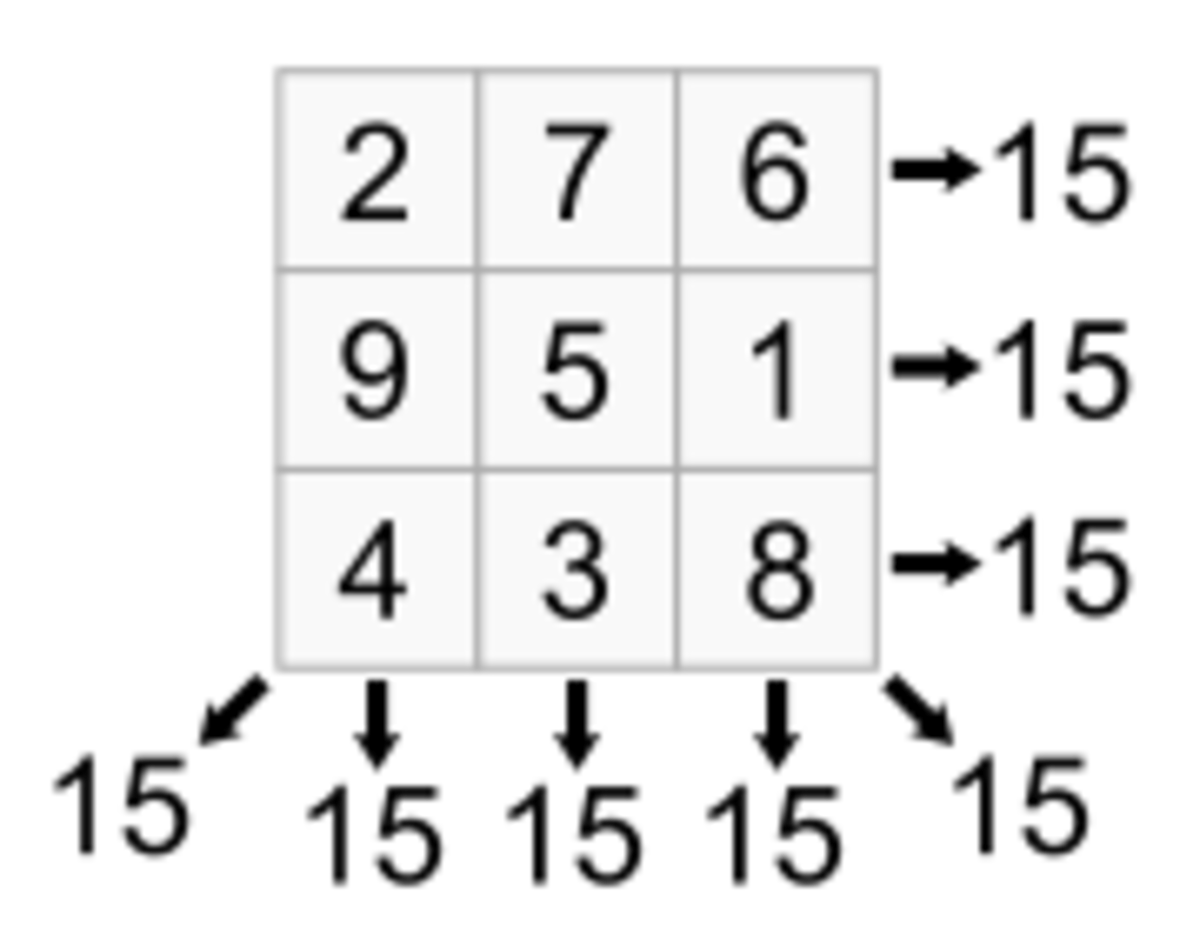Let the magic constant be $30$ , how many different square grids with order $3$ exists?

Assumptions : changing a row determines two different magic squares (e.g. changing the second row $9+5+1$ with $2+11+3$ ) as well as invert the order of numbers (e.g. $3+4+8$ and $4+3+8$ ); the same for columns. Furthermore there is not a limit on the maximum number inside each squares of the grid.