The man in the middle
Fargo, Margo, and Kent each pick a random number between 0 and 1 .
What is the probability that the person that picked the number in the middle, picked a number between 3 1 and 3 2 ?
Round your answer to two decimal places.
The answer is 0.48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Whoa... What a remarkably clear and ingenious approach, David... I love it!
Log in to reply
Thanks! I always enjoy your problems, please keep the coming!
If M is the middle number then, if 0 < x < 1 and δ x > 0 is an infinitesimal, then P [ x < M < x + δ x ] = 3 ! × x × δ x × ( 1 − x − δ x ) ≈ 6 x ( 1 − x ) δ x (one of the values has to be less than x , one has to be greater than x + δ x , while the third has to lie between x and x + δ x . Thus the probability density function of M is f M ( x ) = { 6 x ( 1 − x ) 0 0 < x < 1 o . w . and hence P [ 3 1 < M < 3 2 ] = ∫ 3 1 3 2 6 x ( 1 − x ) d x = 2 7 1 3
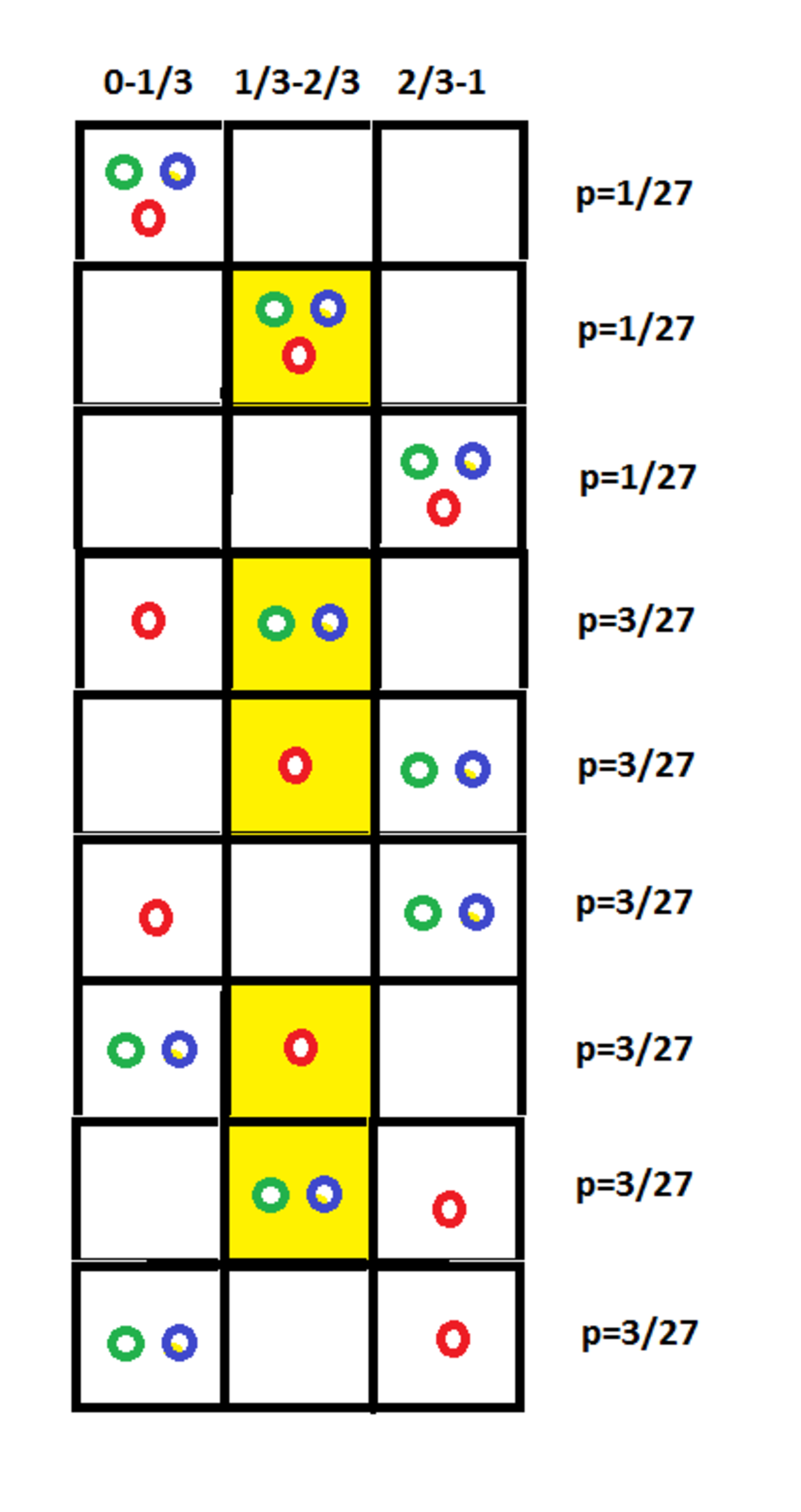
2 7 1 + 2 7 3 + 2 7 3 + 2 7 3 + 2 7 3 = 2 7 1 3
Let Fargo's number be x , Margo's be y , and Kent's be z . Then their numbers can be plotted as a point on an x y z -coordinate system inside a unit cube. Divide the unit cube into 2 7 congruent 3 1 × 3 1 × 3 1 smaller cubes (like a Rubik's cube). Then the following green cubes have a middle coordinate between 3 1 and 3 2 , and the following red cubes do not.
Since 1 3 out of 2 7 cubes are green, the probability is 2 7 1 3 ≈ 0 . 4 8 .