The Maximum Possible Value of P

Algebra Level 1

Place the ten integers 2 through 11 into the ten squares such that the sum of the numbers in each $2 \times 2$ square is the same value, $P.$

What is the maximum possible value of $P?$

26 27 28 29

8 solutions

Eric Chen
Jun 30, 2018

From the problem,we can know that $3P=a+b+c+2d+e+2f+g+h+i+j$ .
Because $a$ through $j$ are all positive integers, $3P$ is also a positive integer.
Therefore $3P$ is a multiplie of 3. Then $a+b+c+2d+e+2f+g+h+i+j$ is a multiplie of 3,too.
$a$ through $i$ corresponds to 2 through 11,therefore $a+b+c+…+h+i=2+3+4+… +10+11=65$ .
Then $(65+d+f)$ is a multiplie of 3.
Therefore $(d+f)_{\text{max}}=9+10=19$ .(Many persons ask me why I don't choose 10 and 11.I have already said that $3P$ is a multiplie of 3 and it is also a integer.So $P$ is also a integer. If I choose 10 and 11,the value will be a decimal. ) And $3P_{\text{max}}=65+(d+f)_{\text{max}}=65+19=84$ .
Therefore $P_{\text{max}}=84÷3=\boxed {28}.$

Here is an example to show that 28 is possible:

Sorry, most and the solution is correct but summation of integers 2 through 11 includes also 1 in this solution (only a typo?). The result of 65 is correct, though.

Henry Kvist - 2 years, 11 months ago

Thank you for your reminding.This is a mistake and I will correct it. And 2+3+4+…+11=65,that is right.

Eric Chen - 2 years, 11 months ago

Gr8 solution, I couldn’t find a way to mathematically approach it, I get it when i see it, but getting from that problem to see a way to solve it isn’t coming easily, I’m old and self educated but I got it by trial and error quite quickly - but that’s not the point here!!

Anyways - I get you right up till the line • (d+f)max = 9 + 10 • I lost you ... Why does ‘d = 8’ ? Why does ‘f = 10’ ? That line just comes out of nowhere to me. I probably shouldn’t do the intermediate ones. Cheers

Michael Leslie Troth - 2 years, 11 months ago

Stumped me also for a while. I think it's because 19+65=84 is divisible by three but 21+65=86 isn't. And this was required in the last sentence. Also, it has to be as big as possible. So that's why 9 and 10 (but 11 and 10 don't fill the requirements).

P.S. Sorry if this is incomprehensible, English isn't my first language or even the second.

Henry Kvist - 2 years, 11 months ago

@Henry Kvist - I give a mathematical proof in a separate comment, that Pmax = 4(a + 5), where a = the first integer in the 10-integer string of consecutive integers. It also demonstrates that maximum values must be (a + 7) and (a + 8) or 9 and 10. My method is so powerful that it is easy to extend it to four 2x2 squares. Just for fun, I show a filled-in grid for the extended problem!

Albert Fisher - 2 years, 11 months ago

@Michael Owen - I give a mathematical proof in a separate comment, that Pmax = 4(a + 5), where a = the first integer in the 10-integer string of consecutive integers. It also demonstrates that maximum values must be (a + 7) and (a + 8) or 9 and 10. My method is so powerful that it is easy to extend it to four 2x2 squares. Just for fun, I show a filled-in grid for the extended problem!

Albert Fisher - 2 years, 11 months ago

very interesting solution

Laura Gao - 2 years, 11 months ago

I think the common terminology is "a multiple of 3" rather than "... multiplier ..."

Tom Verhoeff - 2 years, 11 months ago

from collections import Counter

def sum_to_n(n, size, limit=None):
    """Produce all lists of `size` positive integers in decreasing order
    that add up to `n`."""
    if size == 1:
        yield [n]
        return
    if limit is None:
        limit = n
    start = (n + size - 1) // size
    stop = min(limit, n - size + 1) + 1
    for i in range(start, stop):
        for tail in sum_to_n(n - i, size - 1, i):
            yield [i] + tail


for tot in range(30,20,-1):
    combos = []            
    for partition in sum_to_n(tot, 4):
        if len(set(partition)) == 4 and max(partition) <= 11 and min(partition) >=2:
            combos.append(partition)      

    for i in combos:
        picked = i
        most_comm = []
        for j in combos:
            x = len(list(set(i).intersection(j)))
            y = len(list(set(picked).intersection(j)))
            z = len(list(set(most_comm).intersection(j)))
            if x == 1 and y == 1 and z == 0:
                picked += j
                count = Counter(picked)
                most_comm = [key for key in count.keys() if (count[key] == max(count.values()))]
                if len(set(picked)) == 10 and len(most_comm) == 2:
                    k = map(lambda x: picked[4*x:(x+1)*4], range (3))
                    print 'Tot = %d; values = %s; Common corners = %s' %(tot, k, most_comm)
    print

Tot = 28; values = [[10, 8, 6, 4], [10, 9, 7, 2], [11, 9, 5, 3]]; Common corners = [9, 10]
Tot = 28; values = [[10, 8, 7, 3], [10, 9, 5, 4], [11, 9, 6, 2]]; Common corners = [9, 10]

Tot = 27; values = [[9, 8, 7, 3], [10, 7, 6, 4], [11, 9, 5, 2]]; Common corners = [7, 9]
Tot = 27; values = [[10, 7, 6, 4], [10, 9, 5, 3], [11, 8, 6, 2]]; Common corners = [6, 10]
Tot = 27; values = [[10, 8, 5, 4], [10, 9, 6, 2], [11, 7, 6, 3]]; Common corners = [6, 10]
Tot = 27; values = [[10, 9, 5, 3], [11, 7, 5, 4], [11, 8, 6, 2]]; Common corners = [5, 11]

Tot = 26; values = [[8, 7, 6, 5], [10, 9, 5, 2], [11, 8, 4, 3]]; Common corners = [5, 8]
Tot = 26; values = [[9, 7, 6, 4], [10, 8, 6, 2], [11, 7, 5, 3]]; Common corners = [6, 7]
Tot = 26; values = [[9, 8, 5, 4], [10, 8, 6, 2], [11, 7, 5, 3]]; Common corners = [5, 8]
Tot = 26; values = [[10, 7, 6, 3], [10, 9, 5, 2], [11, 8, 4, 3]]; Common corners = [3, 10]
Tot = 26; values = [[10, 8, 6, 2], [10, 9, 4, 3], [11, 7, 5, 3]]; Common corners = [3, 10]

Tot = 25; values = [[9, 7, 6, 3], [10, 6, 5, 4], [11, 8, 4, 2]]; Common corners = [4, 6]
Tot = 25; values = [[9, 8, 6, 2], [10, 6, 5, 4], [11, 7, 4, 3]]; Common corners = [4, 6]

Tot = 24; values = [[9, 6, 5, 4], [10, 7, 4, 3], [11, 8, 3, 2]]; Common corners = [3, 4]
Tot = 24; values = [[9, 8, 4, 3], [10, 6, 5, 3], [11, 7, 4, 2]]; Common corners = [3, 4]
Tot = 24; values = [[9, 8, 5, 2], [10, 6, 5, 3], [11, 7, 4, 2]]; Common corners = [2, 5]
Tot = 24; values = [[10, 8, 4, 2], [9, 7, 5, 3], [11, 6, 4, 3]]; Common corners = [3, 4]

Michael Fitzgerald - 2 years, 11 months ago

Brilliant, deleted my solution by accident and could not repost. Can this be posted as a solution please?

Michael Fitzgerald - 2 years, 11 months ago

I estimated 65+10+11 = 86 would not fit an integer P., so the solution has to be the next lower multiple of 3, 84.

Olaf Doschke - 2 years, 10 months ago

Nice. Now it would be interesting to know how many solutions there are...

Varsha Dani - 2 years, 8 months ago

Jeremy Galvagni
Jul 8, 2018

The numbers 2 through 11 sums to 65. The highest sum of the three 2x2 squares would come from raising this sum even more. Only two boxes are used twice, so try putting 10 and 11 in them. Now the total is 86. Each 2x2 would have to be one-third of this, but 86/3 is 28.667, not an integer. So 29 is ruled out.

Is 28 possible? 28*3=84. So the two duplicate boxes would have to sum to 84-65=19. Thre are two choices. Let's try 9 and 10.

The green 2x2 needs two more numbers that sum to 28-19=9. Let's try 4 and 5.

We are left with 2,3,6,7,8,11.

The 2x2 with the 10 already filled needs three of the numbers left that sum to 28-10=18. Let's try 3,7,8.

We are left with 2,6,11 which of course sum with 19 to complete the last 2x2 box with a sum of $\boxed{28}$ .

This was easier to follow then the rest. Great intuition

Lincoln Francis - 2 years, 11 months ago

Binky Mh
Jul 9, 2018

Each section contains $4$ numbers which add up to $P$ , so the sum of all $12$ numbers is equal to $3\times P$ .

As two of the squares are used by multiple sections, if we want to maximise $3\times P$ , We need to maximise the duplicate numbers.

However, as $P$ must be an integer, the sum of all squares must be a multiple of $3$ . This means the highest possible pair of numbers to go in these squares must add to $19$ , since any higher would make the sum not a multiple of $3$ . With this, we can now work out our maximum:

$3\times P=(2+3+4+5+6+7+8+9+10+11)+19=84$ $P=\boxed{28}$

Very nicely written, though of course you must also show an construction of P=28. As of yet you have only shown the solution is at most 28.

Alex Li - 2 years, 11 months ago

As other higher up solutions had presented constructions of their own, I felt I'd just be repeating them.

Binky MH - 2 years, 11 months ago

I agree, that would be repetitious, but I think it's worthwhile to reference those solutions so other people realize that it is a necessary step

Alex Li - 2 years, 11 months ago

from collections import Counter

def sum_to_n(n, size, limit=None):
    """Produce all lists of `size` positive integers in decreasing order
    that add up to `n`."""
    if size == 1:
        yield [n]
        return
    if limit is None:
        limit = n
    start = (n + size - 1) // size
    stop = min(limit, n - size + 1) + 1
    for i in range(start, stop):
        for tail in sum_to_n(n - i, size - 1, i):
            yield [i] + tail


for tot in range(30,20,-1):
    combos = []            
    for partition in sum_to_n(tot, 4):
        if len(set(partition)) == 4 and max(partition) <= 11 and min(partition) >=2:
            combos.append(partition)      

    for i in combos:
        picked = i
        most_comm = []
        for j in combos:
            x = len(list(set(i).intersection(j)))
            y = len(list(set(picked).intersection(j)))
            z = len(list(set(most_comm).intersection(j)))
            if x == 1 and y == 1 and z == 0:
                picked += j
                count = Counter(picked)
                most_comm = [key for key in count.keys() if (count[key] == max(count.values()))]
                if len(set(picked)) == 10 and len(most_comm) == 2:
                    k = map(lambda x: picked[4*x:(x+1)*4], range (3))
                    print 'Tot = %d; values = %s; Common corners = %s' %(tot, k, most_comm)
    print

Tot = 28; values = [[10, 8, 6, 4], [10, 9, 7, 2], [11, 9, 5, 3]]; Common corners = [9, 10]
Tot = 28; values = [[10, 8, 7, 3], [10, 9, 5, 4], [11, 9, 6, 2]]; Common corners = [9, 10]

Tot = 27; values = [[9, 8, 7, 3], [10, 7, 6, 4], [11, 9, 5, 2]]; Common corners = [7, 9]
Tot = 27; values = [[10, 7, 6, 4], [10, 9, 5, 3], [11, 8, 6, 2]]; Common corners = [6, 10]
Tot = 27; values = [[10, 8, 5, 4], [10, 9, 6, 2], [11, 7, 6, 3]]; Common corners = [6, 10]
Tot = 27; values = [[10, 9, 5, 3], [11, 7, 5, 4], [11, 8, 6, 2]]; Common corners = [5, 11]

Tot = 26; values = [[8, 7, 6, 5], [10, 9, 5, 2], [11, 8, 4, 3]]; Common corners = [5, 8]
Tot = 26; values = [[9, 7, 6, 4], [10, 8, 6, 2], [11, 7, 5, 3]]; Common corners = [6, 7]
Tot = 26; values = [[9, 8, 5, 4], [10, 8, 6, 2], [11, 7, 5, 3]]; Common corners = [5, 8]
Tot = 26; values = [[10, 7, 6, 3], [10, 9, 5, 2], [11, 8, 4, 3]]; Common corners = [3, 10]
Tot = 26; values = [[10, 8, 6, 2], [10, 9, 4, 3], [11, 7, 5, 3]]; Common corners = [3, 10]

Tot = 25; values = [[9, 7, 6, 3], [10, 6, 5, 4], [11, 8, 4, 2]]; Common corners = [4, 6]
Tot = 25; values = [[9, 8, 6, 2], [10, 6, 5, 4], [11, 7, 4, 3]]; Common corners = [4, 6]

Tot = 24; values = [[9, 6, 5, 4], [10, 7, 4, 3], [11, 8, 3, 2]]; Common corners = [3, 4]
Tot = 24; values = [[9, 8, 4, 3], [10, 6, 5, 3], [11, 7, 4, 2]]; Common corners = [3, 4]
Tot = 24; values = [[9, 8, 5, 2], [10, 6, 5, 3], [11, 7, 4, 2]]; Common corners = [2, 5]
Tot = 24; values = [[10, 8, 4, 2], [9, 7, 5, 3], [11, 6, 4, 3]]; Common corners = [3, 4]

Michael Fitzgerald - 2 years, 11 months ago

I wrote a similar and less elegant solution in Java. :)

package test;

import java.util.Random;

public class Test {

public static void main(String[] args) {

    int max = 0;
    for(int i=0; i<100000; i++) {
        max = guess(max);
    }
}

private static int guess(int max) {
    int current[] = getRandomNumbers();

    int red = current[0] + current[1] + current[2] + current[3];
    int green = current[3] + current[4] + current[5] + current[6];
    int blue = current[6] + current[7] + current[8] + current[9];

    if(red == green && green == blue && red > max) {
        for(int i=0; i<10; i++) {
            System.err.print(" "+current[i]);
        }
        System.err.println("\n  red:"+red+"\n  green:"+green+"\n  blue:"+blue);
        return red;
    }

    return max;
}

private static int[] getRandomNumbers() {
    Random r = new Random();
    int current[] = new int[10];
    for(int i=0; i<10; i++) {

        again:
        while(true) {
            int n = r.nextInt(12);

            if(n < 2) {
                continue again;
            }

            for(int j=0; j<i; j++) {
                if(n == current[j]) {
                    continue again;
                }
            }
            current[i] = n;
            break;
        }
    }

    return current;
}

}

Output: 6 8 3 9 11 2 4 5 10 7 red:26 green:26 blue:26 8 11 2 6 7 4 10 3 5 9 red:27 green:27 blue:27 3 4 10 11 7 2 8 5 9 6 red:28 green:28 blue:28

Kurt Zoglmann - 2 years, 11 months ago

Python is the way to go!

Michael Fitzgerald - 2 years, 11 months ago

Deleted my original solution by accident and could not repost. Brilliant...can this be posted as a solution please?

Michael Fitzgerald - 2 years, 11 months ago

Murat Tepe
Jul 15, 2018

2+3+4+5+6+7+8+9+10+11=65 When we fill in the squares two numbers are repeated in the intersected squares. Therefore we need to add two of the numbers to 65 and the result will be divisible by three. The highest possible pair is 11 and 8 or 10 and 9 which makes 3P equal to 84. Therefore P is 28.

But you need to additionally show that 28 is in fact possible. Fortunately for you, it is :)

Varsha Dani - 2 years, 8 months ago

Mickaël Durand
Jul 9, 2018

Let S be the sum of the sums of the 2×2 squares. To maximize S without the constraint of equality, you must place 10 and 11 in the two joint cells. Then the maximum of S is 86 ( $\sum\limits_{i=2}^{11} i + 10 + 11 = 86$ ) .

It proves that $P <= \frac{86}{3} \approx 28.7 \implies P \leq 28$

You can easily find a solution that verify P = 28. (with 10 and 9 in the joint cells, because $S = \sum\limits_{i=2}^{11} i + 10 + 9 = 3 * 28$ ) .

Albert Fisher
Jul 13, 2018

Pmax = 4(a + 5), where "a" = the first integer in the 10-integer string. The approach is to find the maximum values that can go into the two overlapping boxes in the green square that are “shared” by the other two squares: call these two values “x” and “y.”

Since each square individually sums to P, the 12 values in all three squares (the 10 given numbers plus two numbers that are repeated as “x” and “y”) sum to 3P.

In general, for any sequence of ten consecutive integers, we can write:

3P = a + (a + 1) + (a + 2) +…+ (a + 7) + (a + 8) + (a + 9) + x + y

3P = 10a + [1 + 2 + 3 +…+ 7 + 8 + 9) = 10a + (9)(10)/2 + x + y = 10a + 45 + x + y

For “x” and “y,” we need the two largest values from the string that will make the entire expression divisible by three.

All possible choices for “x” and “y” will add two more “a’s,” for a total of 12a. Since 45 is evenly divisible by three, we need two values whose constant terms will add to a number that is also evenly divisible by three. By inspection, the two largest values are x = a + 7 and y = a + 8:

3P = 10a + 45 + (a + 7) + (a + 8) = 10a + 2a + 45 + 15 = 12a + 60 = 12(a + 5)

Dividing by three:

P = 4(a + 5)

The derivation also shows that, for maximum P, “x” and “y” will always be the eighth and ninth integers in the string of ten integers.

For the specific problem, “x” and “y” are 9 and 10, so the other two values in the green square must sum to 9. There are three ways they can sum to 9: (4,5), (3,6), and (2,7). The remaining six integers sum to 65 - 28 = 37. Divide them into two groups of three, one group summing to 18 and the other group summing to 19. Put the three numbers summing to 18 with the 10, and the three numbers summing to 19 with the 9. Here are the three basic distributions:

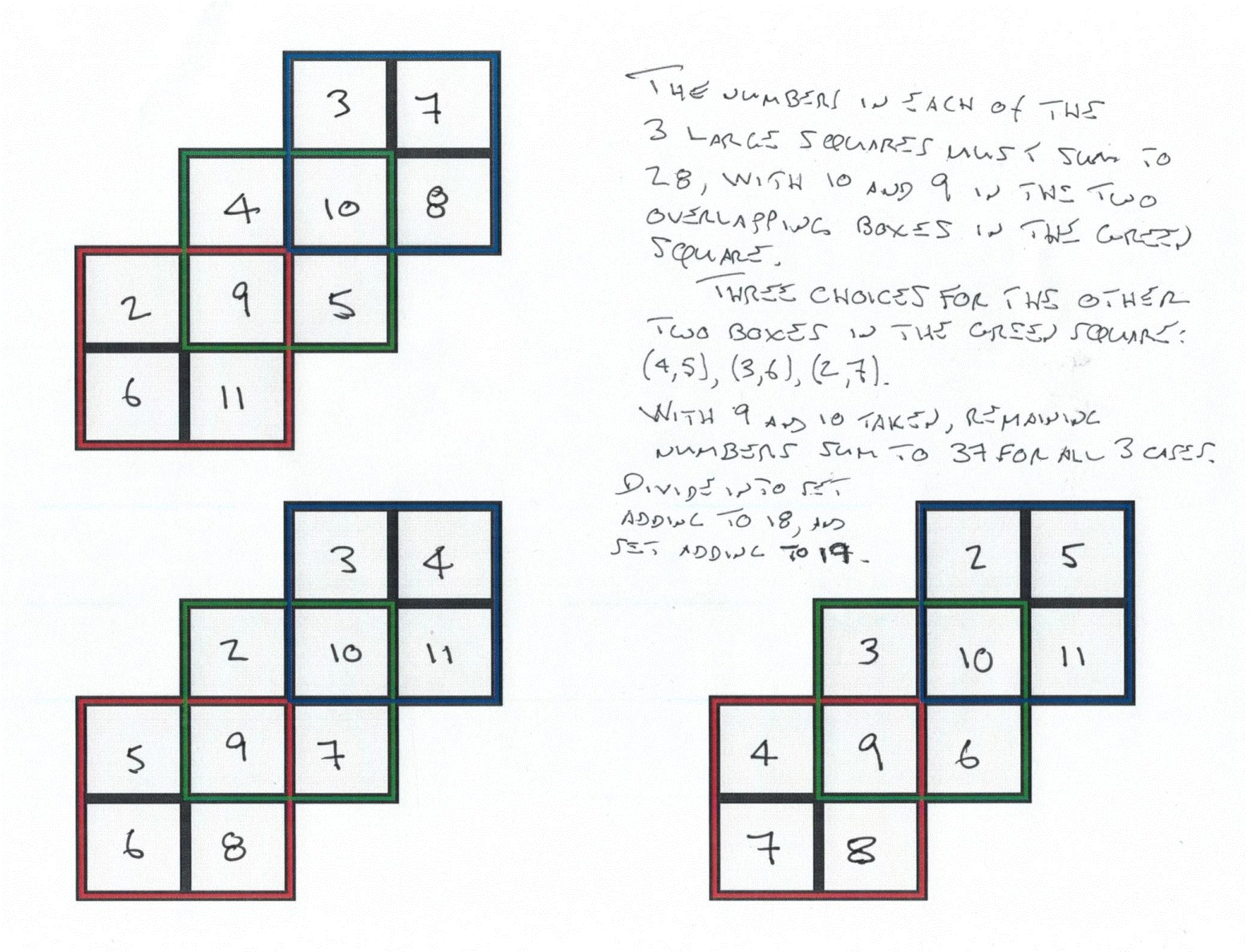
There are two other (non-maximum) values, “P - 4” and “P - 2:” in this case, 24 and 26.

Use (a + 1) and (a + 2) to get P = 24, and (a + 4) and (a + 5) to get P = 26.

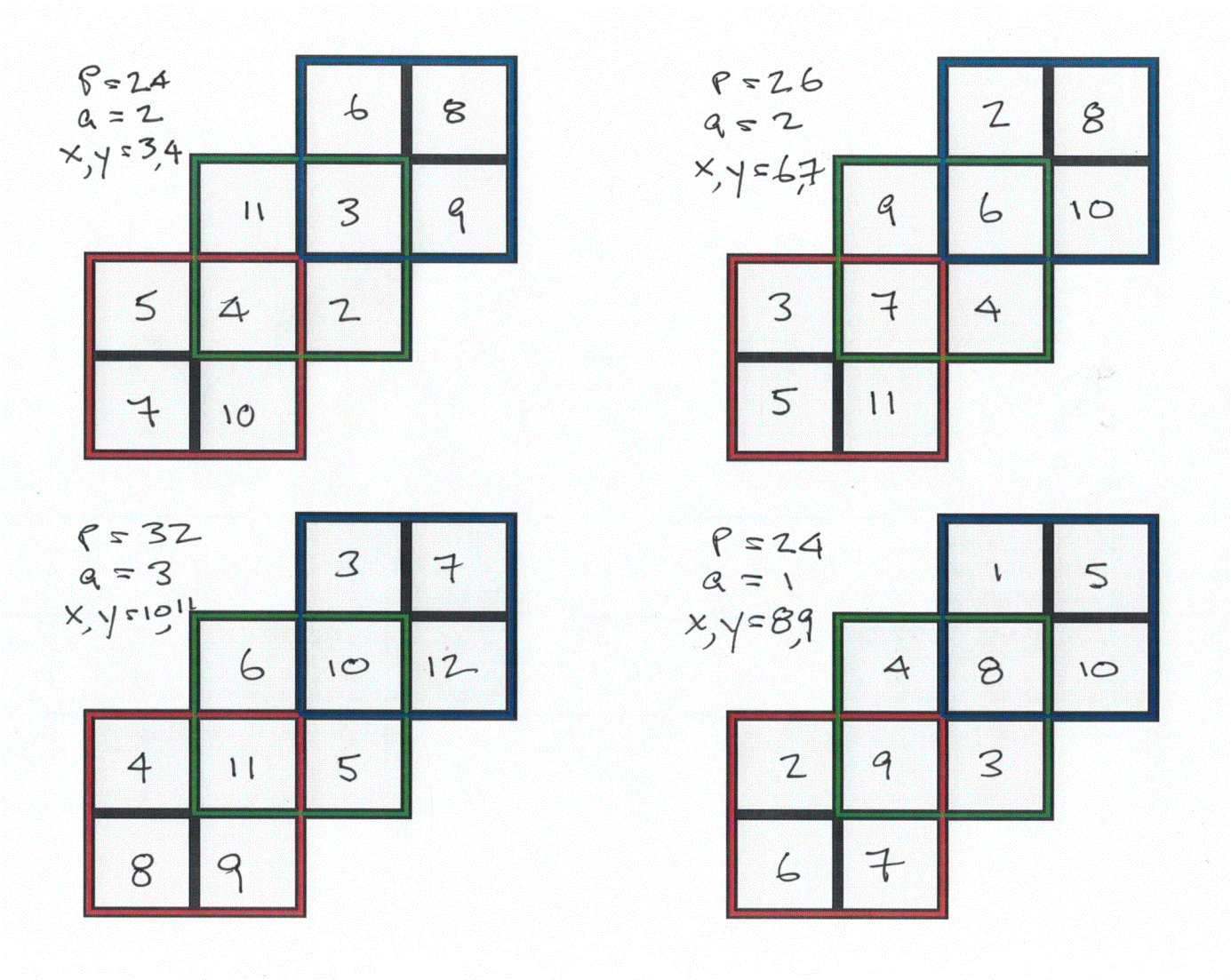
Here are solutions for four cases: P = 24 (a = 2); P = 26 (a = 2); P = 32 (a = 3); P = 24 (a = 1).

This method is so powerful that it is easy to extend the concept to four overlapping 2x2 squares: P = 4a + 27 = 35. Here is a solution:

Pierre Morin
Jul 12, 2018

"I found with a excel macro that the value of P may be 24 to 28; and that there are 7200 possibilities (1152 possibilities if the sum is 28)"

@Pierre Morin – I presume that your macro shows only even values of P: 24, 26, and 28. I have a separate posting that shows Pmax = 4(a + 5), where “a” = the first integer in the 10-integer string. I also show actual distributions of integers 2-11 within the three interlocking squares that are organized (non-maximally) such that P = 24 and P = 26.

Albert Fisher - 2 years, 11 months ago

Carlos Moreno Serrano
Jul 10, 2018

You can think the problem in terms of weights that you are placing on three plates or grids. You can make these plates balance and have the same average weight.

As we have to use all numbers from 2 to 11, I did like Gauss and separated all numbers into pairs that would add to 13 (2+11, 3+10, 4+9, 5+8, 6+7). Each 2x2 matrix would use two of these pairs, so on average P would be 13x2=26, however, as there are two overlaps, we can reuse two numbers. We want to maximise the value of P, so we re-use two of the highest numbers: 9 and 10. If we had three separate 2x2 matrices, then we would use 1 and 12 to fill the gaps, for example. That would give us 13 again. However, as we are re-using 9 and 10, that gives us 19, so the "excess" is 19-13=6. As we have three 2x2 matrices, we divide this "extra weight" among the three and the average would increase by two units from P=26 to P=28.

Please note how Eric Chen's solution chose 9 and 10 arbitrarily. Why not choose to re-use 10 and 11 instead? This is because we won't find a P that is an integer. If you follow my method, you can see that choosing 10 and 11 would give 21. If we deduct it from the average "weight" of a pair of numbers, which is 13 we would get 21-13 = 8, which is not divisible by 3 and P would not be an integer.

What could be the minimum value of P? Which numbers should we choose to re-use?

Using my method, we know that the average weight of a pair is 13, so we choose the minimum pair of numbers 2 and 3, which would reduce the average weight by 13 - (2+3) = 13 - 5 = 8, which is not divisible by 3. Let's try with 3 and 4, 13 - (3+4) = 13 - 7 = 6, which is divisible by 3. This means that the minimum P would be 2 units less than the original 26. So minimum P would be 24 and the re-used numbers would be 3 and 4.

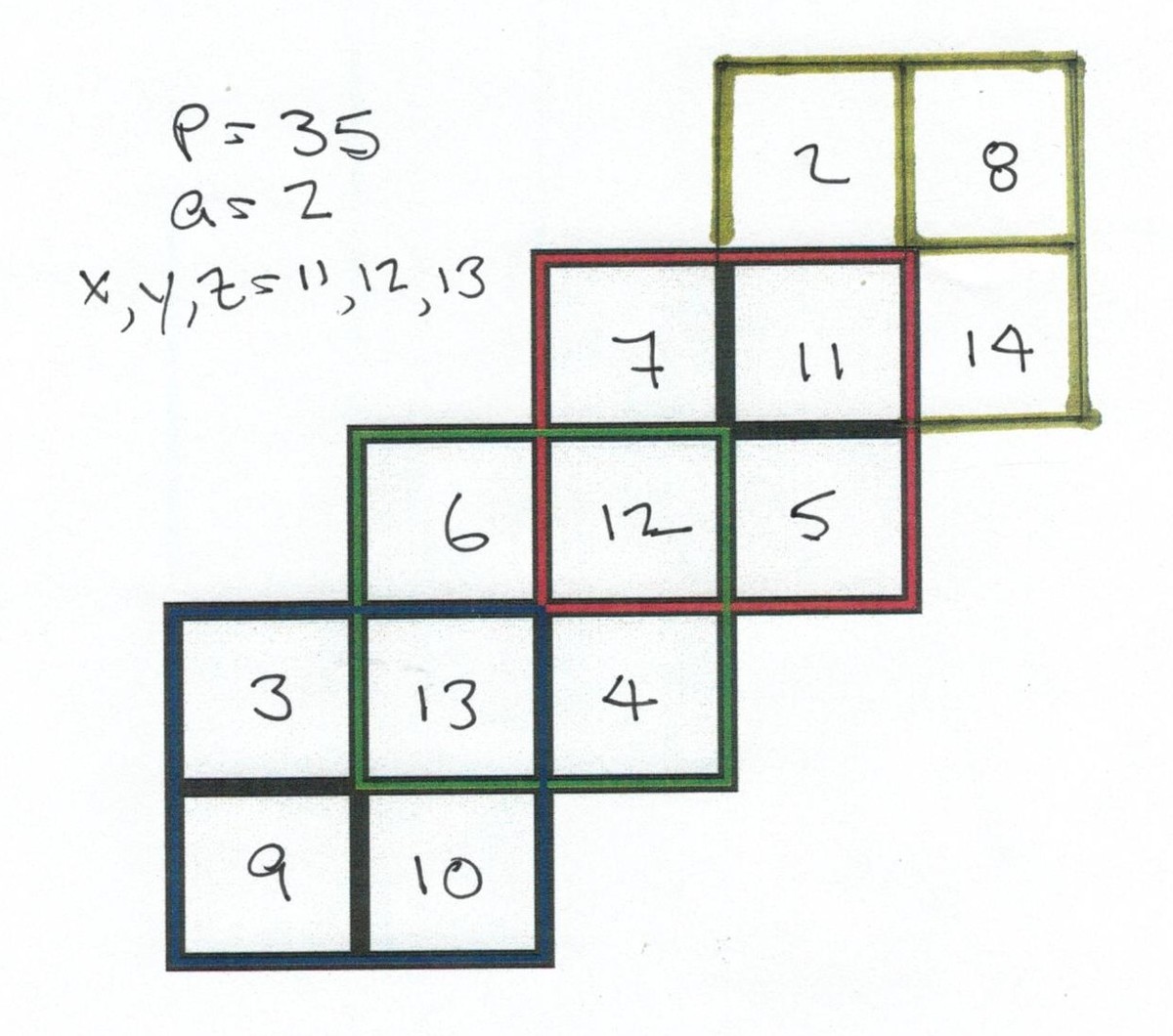
BONUS If you do it for 4 2x2 matrices, you would get 3 intersections. If you follow the same rules, you would fill them with numbers from 2 to 14 and you would repeat 3 of those numbers. The repeated numbers are 11, 12 and 13 (again one less than the maximum 14, like for the previous case it was one less than 11) and average P gets improved by the number of intersections from P=32 to P=35 and for the minimum P we would repeat 3, 4 and 5 and obtain a minimum P=29.

I have not tried with 5 2x2 matrices, but I can see a pattern forming here with Pmax and Pmin being increased and decreased 1 per intersection respectively.

@Carlos Moreno Serrano – Your method yields some very useful results. I took a different approach that supports your (Bonus) extension to four 2x2 interlocking squares, proposing 11, 12, and 13 as the repeated numbers. Here is what I did (I am skipping some details because I cover them in a separate posting):

4P = a + (a + 1) + (a + 2) + (a + 3) +…+ (a + 9) + (a + 10) + (a + 11) + (a + 12) + x + y + z

Where x, y, and z are the repeated numbers.

4P = 13a + (1 + 2 + 3 +…+ 10 + 11 + 12) + x + y + z

4P = 13a + (12)(13)/2 + x + y + z = 13a + (6)(13) + x + y + z

If, as you propose, we use 11, 12, and 13 as the repeated numbers, that translates to x, y, and z as (a + 9), (a + 10), and (a + 11). When we put these values into the above equation:

4P = 13a + (6)(13) + (a + 9) + (a + 10) + (a + 11)

4P = 13a + 78 + 3a + 30 = 16a + 108

Divide by 4:

P = 4a + 27 or P = 35 for a = 2

Which agrees with your conclusion.

My approach is so powerful that it is easy for me to complete the four 2x2 interlocking squares. See my separate posting for a completed grid.

Albert Fisher - 2 years, 11 months ago

The Maximum Possible Value of P

8 solutions

0 pending reports