The Middle Red Square
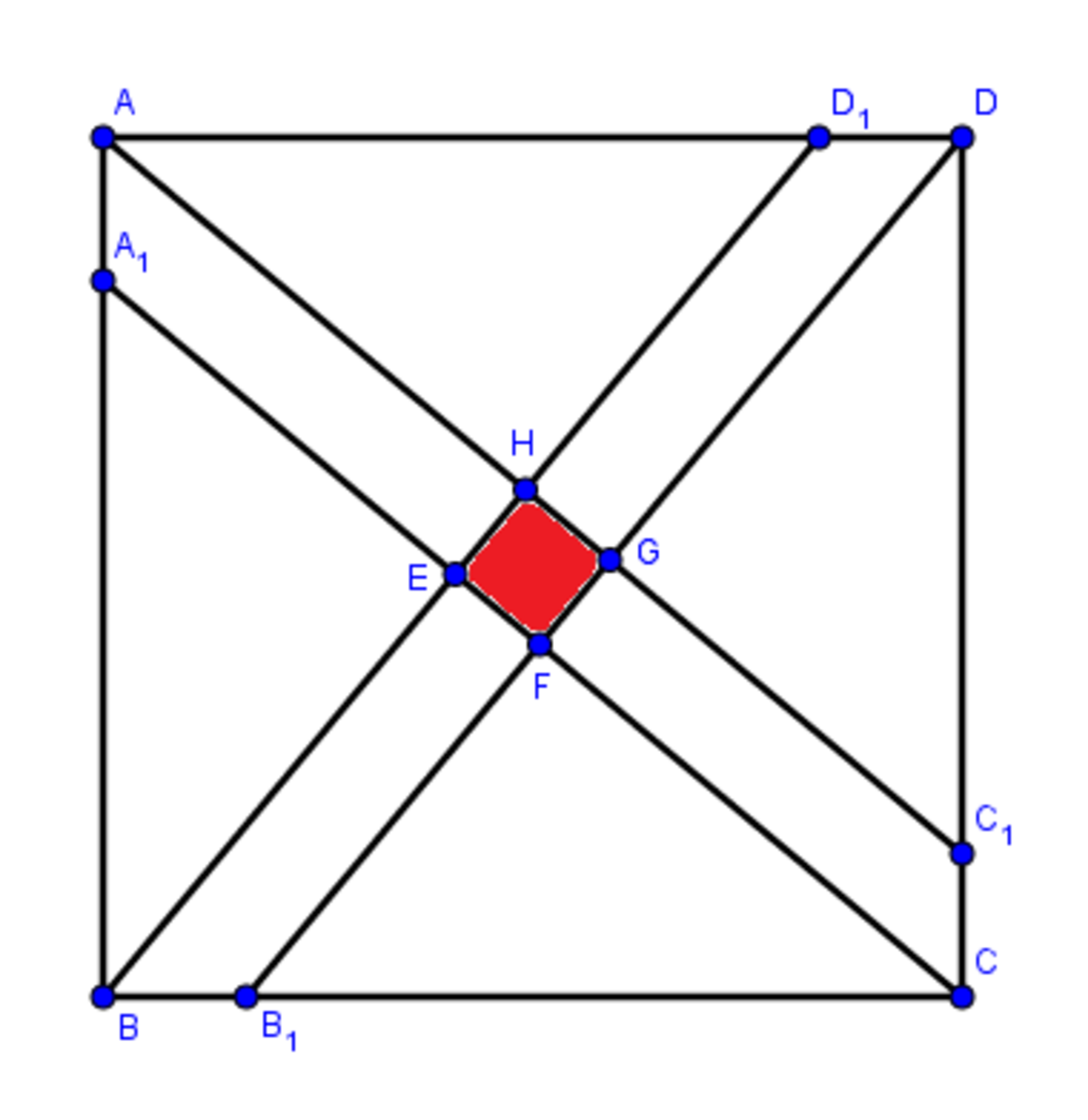 The figure above shows a square
A
B
C
D
.
A
1
,
B
1
,
C
1
,
D
1
lie on
A
B
,
B
C
,
C
D
,
D
A
such that
A
A
1
=
B
B
1
=
C
C
1
=
D
D
1
. If the area of red square
E
F
G
H
is
4
1
1
of the area of square
A
B
C
D
, the ratio
A
A
1
:
A
B
can be represented by
1
:
k
. Find the vaue of
k
.
The figure above shows a square
A
B
C
D
.
A
1
,
B
1
,
C
1
,
D
1
lie on
A
B
,
B
C
,
C
D
,
D
A
such that
A
A
1
=
B
B
1
=
C
C
1
=
D
D
1
. If the area of red square
E
F
G
H
is
4
1
1
of the area of square
A
B
C
D
, the ratio
A
A
1
:
A
B
can be represented by
1
:
k
. Find the vaue of
k
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 .
.
Let the side of A B C D be l , then D D 1 = k l .
It follows that A D 1 = l ( 1 − k 1 ) and, by the pythagorean theorem ,
B D 1 = l 2 + k 2 1 − k 2
Since △ A B D 1 and △ D D 1 K are similar
B D 1 A B = D D 1 K D 1
2 + k 2 1 − k 2 l = k l K D 1 ⟺ K D 1 = k 2 + k 2 1 − k 2 l
Since G H = K D 1 , the ratio of the area of the red square to the area of A B C D is
r = l 2 ( K D 1 ) 2 = 2 k 2 − 2 k + 1 1
In this case the ratio is 4 1 1
2 k 2 − 2 k + 1 1 = 4 1 1
k 2 − k − 2 0 = 0 ⟺ ( k − 5 ) ( k + 4 ) = 0 ⟺ k = 5 , k = − 4
Obviously we discard the negative solution, so the answer is k = 5
Nice solution!
Here is a solution, not by me:
Let A B = 1 , ∠ D 1 B B 1 = α , B B 1 = x ,
then E F = B B 1 s i n α = x s i n α
In △ B 1 C D , s i n α = B 1 D C D = 1 2 + ( 1 − x ) 2 1
∴ Area of square E F G H = E F 2 = x 2 s i n 2 α = 1 2 + ( 1 − x ) 2 x 2 = 4 1 1
2 0 x 2 + x − 1 = 0
( 5 x − 1 ) ( 4 x + 1 ) = 0
∴ x = 5 1 , k = 5